
一、介绍
扩散模型通过稳定的训练过程实现了前所未有的真实性和多样性水平。然而,与 GAN 和 VAE 相比,它们的采样是一个缓慢的迭代过程,通过渐进式去噪将高斯噪声样本转换为复杂的图像。这通常需要数十到数百次昂贵的神经网络评估,限制了作为创意工具的交互性。
为了加快采样速度,以前的方法是将原始多步扩散采样发现的噪声→图像映射提炼为单程学生网络。然而,拟合如此高维、复杂的映射无疑是一项艰巨的任务。一个挑战是,仅仅为了实现学生模型的一次损失计算,就需要运行整个去噪轨迹,成本高昂。最近的方法(渐进性蒸馏,一致性模型)通过逐步增加学生的采样距离来缓解这一问题,而无需运行原始扩散的完整去噪序列。然而,蒸馏模型的性能仍然落后于原始的多步扩散模型。
相比之下,本文提出的不是强制噪声和扩散生成的图像之间的对应关系,而是简单地强制要求学生模型生成的图像看起来与原始扩散模型没有区别。在高层次上,本文的目标与其他分布匹配生成模型(例如 GMMN 或 GAN )具有相同的动机。具体来说,作者对预训练的扩散模型进行微调,不仅可以学习真实数据分布,还可以学习蒸馏生成器生成的假分布。扩散模型可以近似扩散分布上的得分函数,因此可以将去噪扩散输出解释为使图像“更逼真”的梯度方向,或者如果扩散模型是在假图像上学习的, 则输出是朝着“更假”的梯度方向。最后,生成器的梯度更新规则被设计为两者的差异,将合成图像推向更高的真实性和更低的虚假性。一种称为变分分数蒸馏的方法中表明了使用预训练的扩散模型对真实和虚假分布进行建模对于 3D 对象的测试时优化也是有效的。作者的观点认为,类似的方法可以训练整个生成模型。
二、方法
DMD的目标是将给定的预训练扩散去噪器(基本模型 \(\textcolor{blue}{μ_{base}}\))提炼为快速“一步”图像生成器 \(\textcolor{blue}{G_θ}\),无需昂贵的迭代采样过程即可生成高质量图像。作者表明虽然希望从相同的分布中产生样本,但不一定寻求重现精确的映射。
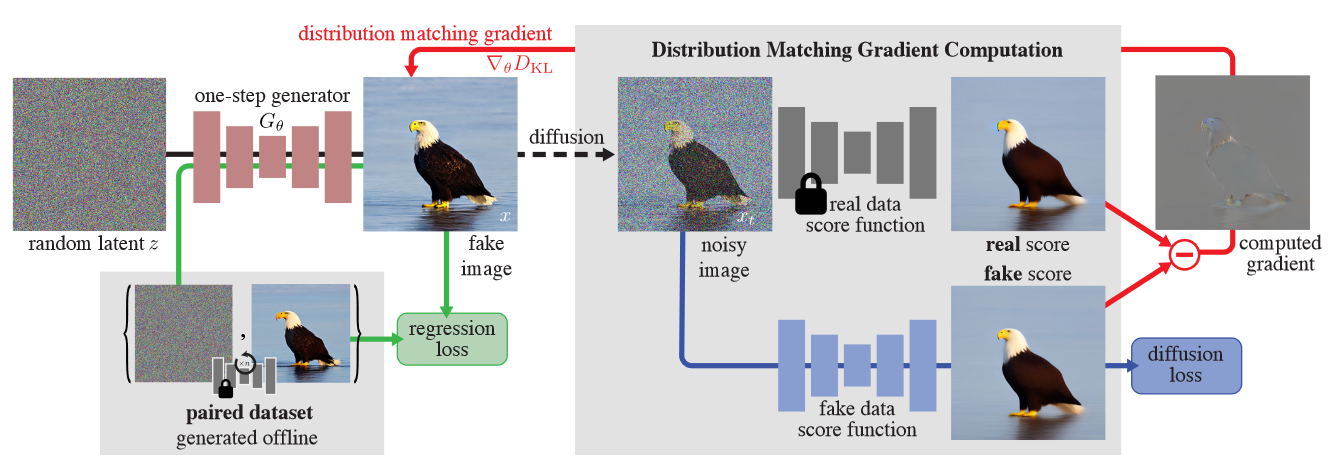
图2:方法概述。训练一步生成器 \(G_θ\) 将随机噪声 \(z\) 映射到逼真的图像中。为了匹配扩散模型的多步采样输出,预先计算了噪声与图像对的集合,并偶尔从集合中加载噪声,并在一步生成器和扩散输出之间强制执行 LPIPS 回归损失。此外,作者为假图像提供分布匹配梯度\(∇_θD_{KL}\)以增强真实感。将随机数量的噪声注入到假图像当中,并将其传递给两个扩散模型,一个在真实数据上进行预训练,另一个在具有扩散损失的假图像上持续训练,以获得其去噪版本。去噪分数(在图中可视化为平均预测)指示使图像更真实或更虚假的方向。两者之间的差异代表了更加真实和更少虚假的方向,并且被反向传播到单步生成器。
1.预训练基础模型和一步生成器
预训练的扩散模型 \(\textcolor{blue}{μ_{base}}\):扩散模型经过训练以逆转高斯扩散过程,该过程逐渐向来自真实数据分布 \(\textcolor{blue}{x_0 ∼ p_{real}}\) 的样本添加噪声,在 \(\textcolor{blue}{T}\) 时间步长内将其转变为白噪声 \(\textcolor{blue}{x_T ∼ N(0, I)}\); 我们使用 \(\textcolor{blue}{T = 1000}\)。扩散模型表示为 \(\textcolor{blue}{μ_{base}(x_t, t)}\)。从高斯样本 \(\textcolor{blue}{x_T}\) 开始,模型迭代地对运行噪声估计 \(\textcolor{blue}{x_t}\) 进行去噪,以时间步 \(\textcolor{blue}{t ∈ \{0, 1, ..., T − 1\}}\) (或噪声级别)为条件,以生成目标数据的样本分配。扩散模型通常需要 10 到 100 秒的步骤才能生成逼真的图像。本文的实现使用来自 EDM 和稳定扩散的预训练模型。
一步生成器:一步生成器 \(\textcolor{blue}{G_θ}\) 具有基础扩散去噪器的架构,但没有时间条件。在训练之前,用基础模型初始化其参数 \(\textcolor{blue}{θ}\),即 \(\textcolor{blue}{G_θ(z) = μ_{base}(z, T − 1), ∀z}\)。
2.分布匹配损失
理想情况下,希望一步生成器能够生成与真实图像无法区分的样本。受 ProlificDreamer 的启发,分别最小化真实和虚假图像分布 \(\textcolor{blue}{p_{real}}\) 和 \(\textcolor{blue}{p_{fake}}\) 之间的 Kullback-Leibler (KL) 差异
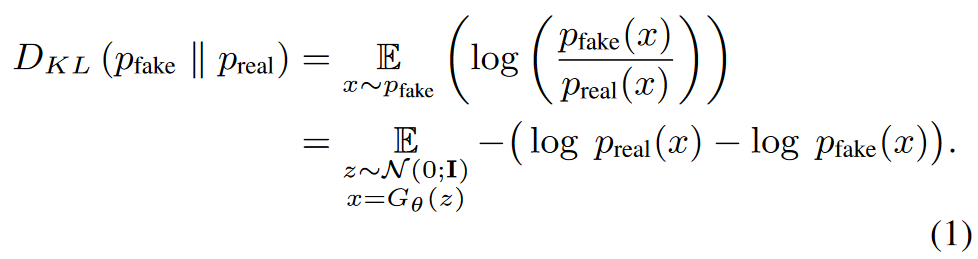
计算概率密度来估计这种损失通常很棘手,但只需要相对于 \(\textcolor{blue}{θ}\) 的梯度即可通过梯度下降来训练生成器。
使用近似分数进行梯度更新:取方程的梯度。 (1)关于生成器的参数:
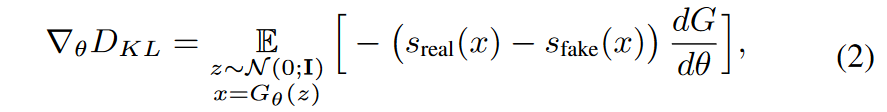
其中 \(\textcolor{blue}{s_{real}(x) = ∇_x\log p_{real}(x)}\), \(\textcolor{blue}{s_{fake}(x) = ∇_x\log p_{fake}(x)}\) 是各个分布的分数。直观上,\(\textcolor{blue}{s_{real}}\) 将 \(\textcolor{blue}{x}\) 移向 \(\textcolor{blue}{p_{real}}\) 的模式,而 \(\textcolor{blue}{−s_{fake}}\) 将它们分开,如图 3(a, b) 所示。计算这个梯度仍然具有挑战性,原因有两个:首先,对于低概率分布样本,分数会发散——特别是 \(\textcolor{blue}{p_{real}}\)会消失,其次,用于估计分数的工具,即扩散模型,仅提供扩散的分数分配。 Score-SDE 为这两个问题提供了答案。
通过使用不同标准差的随机高斯噪声扰动数据分布,我们创建了一系列“模糊”分布,这些分布在环境空间上得到完全支持,因此重叠,因此等式(2)中的梯度定义明确(图 4)。然后,Score-SDE 显示经过训练的扩散模型近似于扩散分布的得分函数。
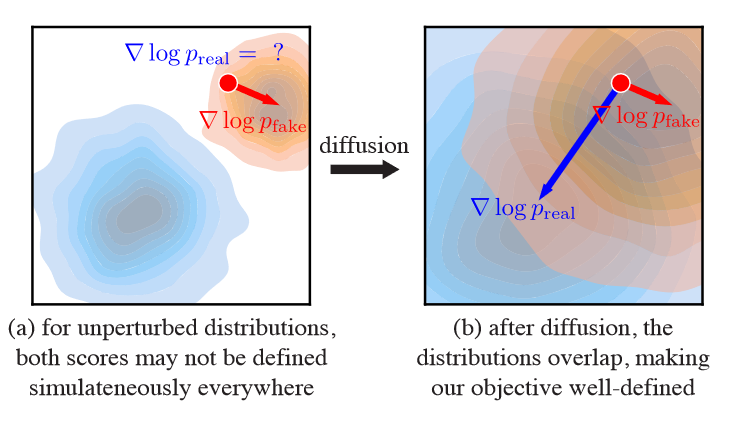
图4:如果没有扰动,真/假分布可能不会重叠 (a)。真实样本仅从真实分数中获得有效梯度,而假样本则从假分数中获得有效梯度。在扩散(b)之后,分布匹配目标在各处都得到了明确的定义。
因此,作者的策略是使用一对扩散去噪器对高斯扩散后的真分布和假分布的分数进行建模。将它们分别定义为 \(\textcolor{blue}{s_{real}(x_t, t)}\) 和 \(\textcolor{blue}{s_{fake}(x_t, t)}\)。扩散样本 \(\textcolor{blue}{x_t ∼ q(x_t|x)}\) 是通过在扩散时间步 \(\textcolor{blue}{t}\) 处向生成器输出 \(\textcolor{blue}{x = G_θ(z)}\) 添加噪声来获得的:
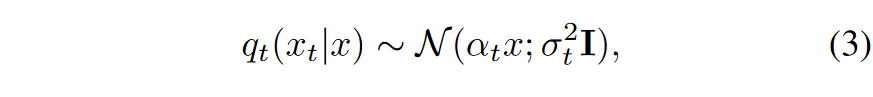
其中 \(\textcolor{blue}{α_t}\) 和 \(\textcolor{blue}{σ_t}\) 来自扩散噪声表。
真实分数:真实分布是固定的,对应于基础扩散模型的训练图像,因此我们使用预训练扩散模型 \(\textcolor{blue}{μ_{base}(x_t, t)}\) 的固定副本对其分数进行建模:
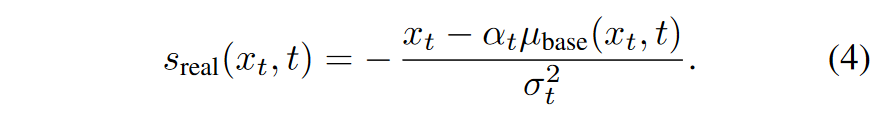
由于我们有\(\textcolor{blue}{q_t(x_t|x) \sim \mathcal{N}(\alpha_t x;\sigma^2_tI)}\),故有\(\textcolor{blue}{q_t(x_t|x) =\frac{1}{\sqrt{2\pi \sigma_t}}e^{-\frac{(x_t-\alpha_t x)^2}{2\sigma_t^2}}}\),将其取对数并对\(\textcolor{blue}{x_t}\)求导,就可获得其分数的表示形式:
\[\large \frac{\partial \log q_t(x_t|x)}{\partial x_t}=\frac{\partial \log \frac{1}{\sqrt{2\pi \sigma_t}}+\partial \log e^{\frac{-(x_t-\alpha_tx)^2}{2\sigma^2_t}}}{\partial x_t}=\frac{\partial \frac{-(x_t-\alpha_tx)^2}{2\sigma_t^2}}{\partial x_t}=-\frac{(x_t-\alpha_tx)}{\sigma_t^2}\]
动态学习的假分数:与真实得分情况相同的方式推导假得分函数:
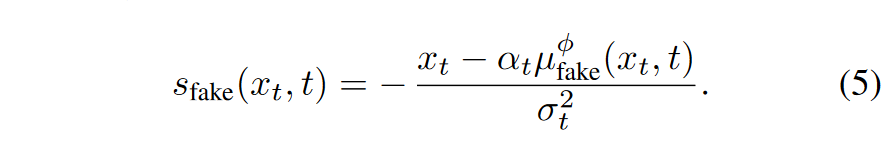
然而,随着生成的样本的分布在整个训练过程中发生变化,动态调整假扩散模型 \(\textcolor{blue}{μ^\phi_{fake}}\) 来跟踪这些变化。从预训练的扩散模型 \(\textcolor{blue}{μ_{base}}\) 初始化假扩散模型,通过最小化标准去噪目标,在训练期间更新参数 \(\textcolor{blue}{\phi}\):
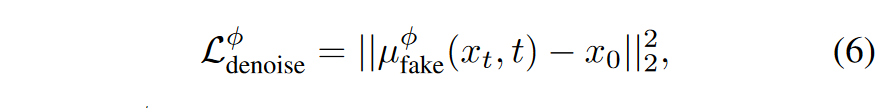
其中 \(\textcolor{blue}{L^\phi_{denoise}}\) 根据扩散时间步长 \(\textcolor{blue}{t}\) 进行加权,使用与基础扩散模型训练期间采用的相同加权策略。
分布匹配梯度更新:最终的近似分布匹配梯度是通过替换方程(2)中的精确分数来获得的。由扰动样本 \(\textcolor{blue}{x_t}\) 上的两个扩散模型定义的模型,并取扩散时间步长的期望:
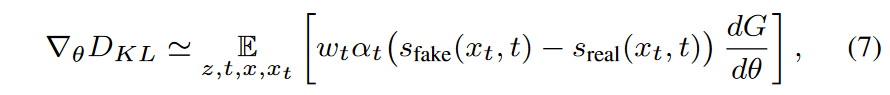
其中 \(\textcolor{blue}{z ∼ N (0; I)、x = G_θ(z)、t ∼ U (T_{min}, T_{max})}\) 和 \(\textcolor{blue}{x_t ∼ q_t(x_t|x)}\)。这里,\(\textcolor{blue}{w_t}\) 是添加的时间相关标量权重,以改善训练动态。作者设计加权因子来标准化不同噪声水平下的梯度大小。具体来说,计算去噪图像和输入之间跨空间和通道维度的平均绝对误差,设置
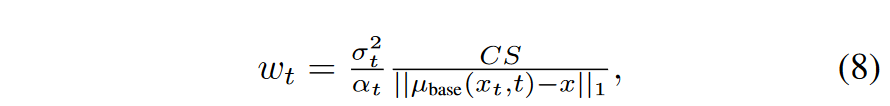
其中 \(\textcolor{blue}{S}\) 是空间位置的数量,\(\textcolor{blue}{C}\) 是通道的数量。遵循 DreamFusion ,我们设置 \(\textcolor{blue}{T_{min} = 0.02 T}\) 和 \(\textcolor{blue}{T_{max} = 0.98 T}\)。
3.回归损失和最终目标
上一节中介绍的分布匹配目标是在 \(\textcolor{blue}{t ≫ 0}\) 时明确定义的,即当生成的样本被大量噪声破坏时。然而,对于少量噪声,\(\textcolor{blue}{s_{real}(x_t, t)}\) 通常变得不可靠,因为 \(\textcolor{blue}{p_{real}(x_t, t)}\) 趋于零。此外,由于分数 \(\textcolor{blue}{∇_x\log(p)}\) 对于概率密度函数 \(\textcolor{blue}{p}\) 的缩放是不变的,因此优化容易受到模式崩溃/下降的影响,其中假分布将更高的总体密度分配给模式的子集。为了避免这种情况,使用额外的回归损失来确保保留所有模式;见图3(b)、(c)。
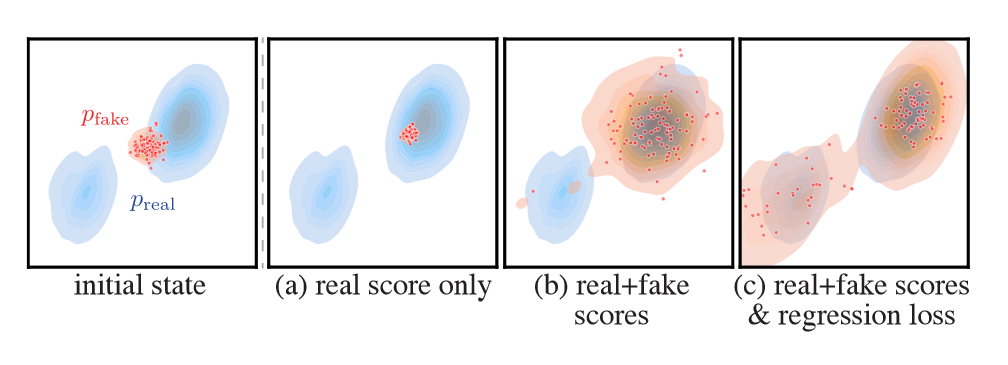
图3:从相同的配置(左)开始优化各种目标会导致不同的结果。 (a) 仅最大化真实分数,假样本全部崩溃到真实分布的最接近模式。 (b) 使用分布匹配目标而不包含回归损失,生成的假数据覆盖了更多的真实分布,但只恢复了最接近的模式,完全丢失了第二个模式。 (c) 完整目标,通过回归损失恢复目标分布的两种模式。
在给定相同输入噪声的情况下,该损失测量生成器和基础扩散模型输出之间的逐点距离。具体来说,构建了随机高斯噪声图像 \(\textcolor{blue}{z}\) 和相应输出 \(\textcolor{blue}{y}\) 的配对数据集 \(\textcolor{blue}{D = \{z, y\}}\),这是通过使用确定性 ODE 求解器对预训练扩散模型 \(\textcolor{blue}{μ_{base}}\) 进行采样而获得的。作者表明即使使用不到 1% 的训练计算生成的少量噪声图像对(例如,在 CIFAR10 的情况下)也可以充当有效的正则化器。回归损失由下式给出:
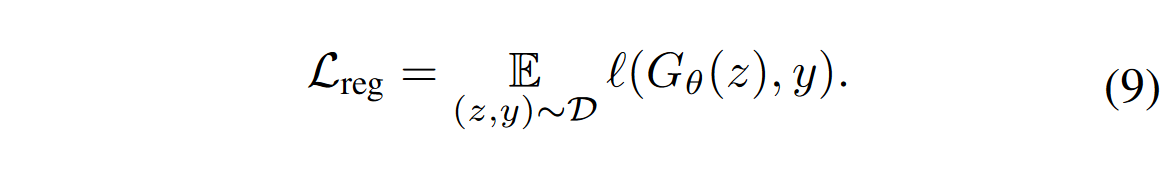
遵循 InstaFlow和一致性模型,使用学习感知图像块相似度 (LPIPS)作为距离函数 \(\textcolor{blue}{\mathcal{l}}\)。
最终目标:网络 \(\textcolor{blue}{μ^\phi_{fake}}\) 使用 \(\textcolor{blue}{L^\phi_{denoise}}\) 进行训练,用于帮助计算 \(\textcolor{blue}{∇_θD_{KL}}\)。对于训练 \(\textcolor{blue}{G_θ}\),最终目标是 \(\textcolor{blue}{D_{KL} + λ_{reg}L_{reg}}\),除非另有说明,否则使用 \(\textcolor{blue}{λ_{reg} = 0.25}\)。梯度 \(\textcolor{blue}{∇_θD_{KL}}\) 的计算由公式 (7)获得,梯度 \(\textcolor{blue}{∇_θL_{reg}}\) 由具有自动微分功能的方程 (9) 获得。作者将这两种损失应用于不同的数据流:用于分布匹配梯度的未配对假样本和用于回归损失的配对示例。算法 1 概述了最终的训练过程。

4.无分类器指导下的蒸馏
无分类器指导被广泛用于提高文本到图像扩散模型的图像质量。该方法也适用于使用无分类器指导的扩散模型。首先通过从引导模型中采样来生成相应的噪声输出对,以构建回归损失 \(\textcolor{blue}{L_{reg}}\) 所需的配对数据集。在计算分布匹配梯度\(\textcolor{blue}{∇_θD_{KL}}\)时,用引导模型的平均预测得出的分数替换真实分数。同时,不修改假分数的公式。用固定的指导尺度来训练一步生成器。
三、实验
1.类条件图像生成
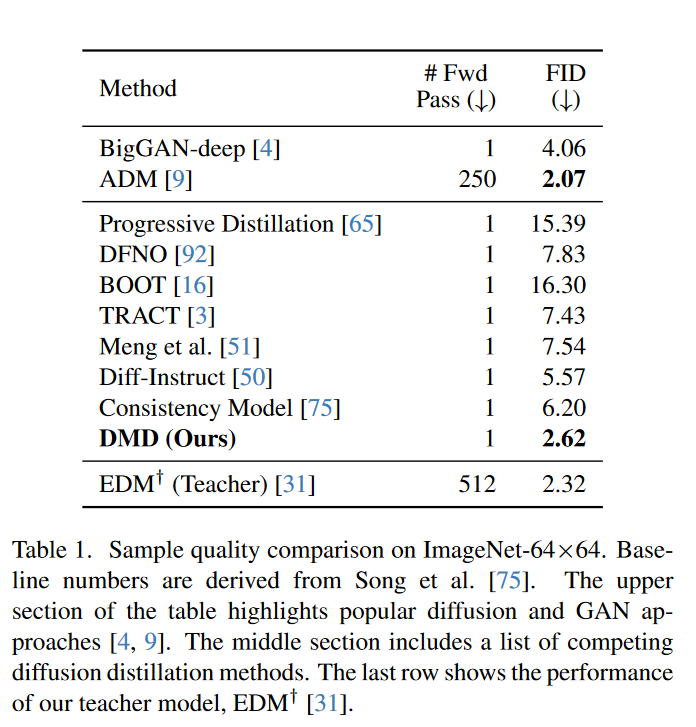
结果如表 1 所示。DMD超越了 BigGAN-deep 等已建立的 GAN 和最近的扩散蒸馏方法,包括一致性模型 和 TRACT 。DMD显着缩小了保真度差距,与原始扩散模型相比,实现了几乎相同的 FID 分数(0.3 以内),同时速度提高了 512 倍。在 CIFAR-10 上,DMD的类条件模型达到了具有竞争力的 FID 2.66。
2.消融研究
首先作者将DMD与两个基线进行比较:一个忽略了分布匹配目标,另一个忽略了DMD框架中的回归损失。表 2总结了结果。在没有分布匹配损失的情况下,基线模型生成的图像缺乏真实感和结构完整性,如图 5 的顶部所示。同样,忽略回归损失会导致训练不稳定和模式崩溃的倾向,从而导致生成图像的多样性减少。图 5 的底部部分说明了这个问题。

图5:训练损失的消融研究,包括分布匹配目标(顶部)和回归损失(底部)。
3.文本到图像生成
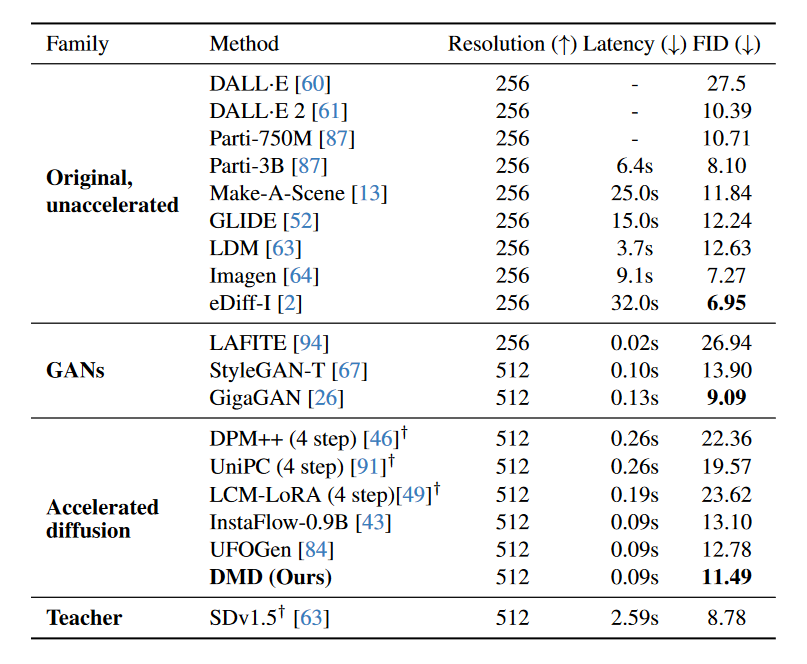
作者使用零样本 MS COCO 来评估DMD在文本到图像生成方面的性能。通过在 LAION-Aesthetics-6.25+ 上提取 Stable Diffusion v1.5 来训练文本到图像模型。使用指导尺度 3,这为基本稳定扩散模型提供了最佳 FID。在由 72 个 A100 GPU 组成的集群上进行训练大约需要 36 小时。表 3 将DMD与最先进的方法进行了比较。DMD展示了优于 StyleGAN-T 的卓越性能,超越了所有其他扩散加速方法,包括高级扩散求解器和扩散蒸馏技术,例如潜在一致性模型、UFOGen、和 InstaFlow。大大缩小了精炼模型和基础模型之间的差距,从 Stable Diffusion v1.5 达到了 2.7 FID 以内,同时运行速度提高了大约 30 倍。通过 FP16 推理,DMD以每秒 20 帧的速度生成图像,从而实现交互式应用程序。
高指导规模扩散蒸馏。对于文本到图像的生成,扩散模型通常以高引导尺度运行以提高图像质量。为了在这种高指导尺度范围内评估本文的蒸馏方法,作者训练了一个额外的文本到图像模型。该模型在 LAION-Aesthetics-6+ 数据集上使用 8 的指导尺度提取 SD v1.5。表 4 将DMD与各种扩散加速方法进行了基准比较。与低引导模型类似,一步生成器显着优于竞争方法,即使它们使用四步采样过程。与竞争方法和基础扩散模型的定性比较如图 6 所示。
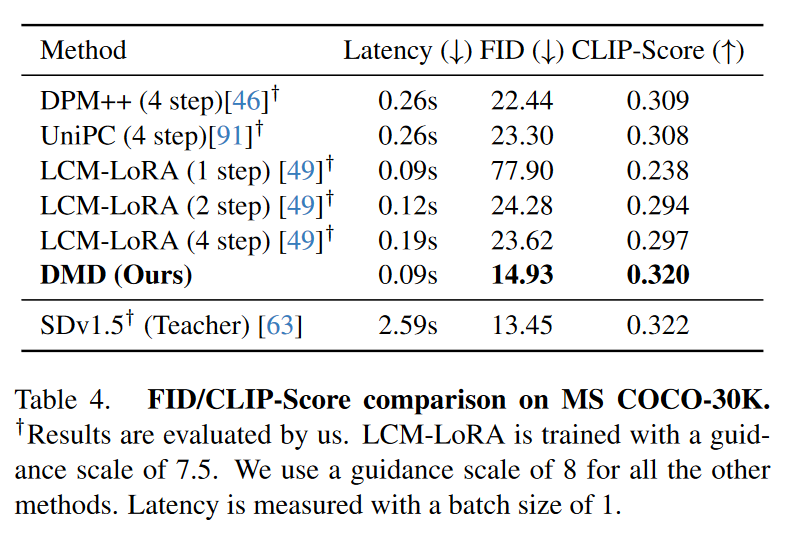
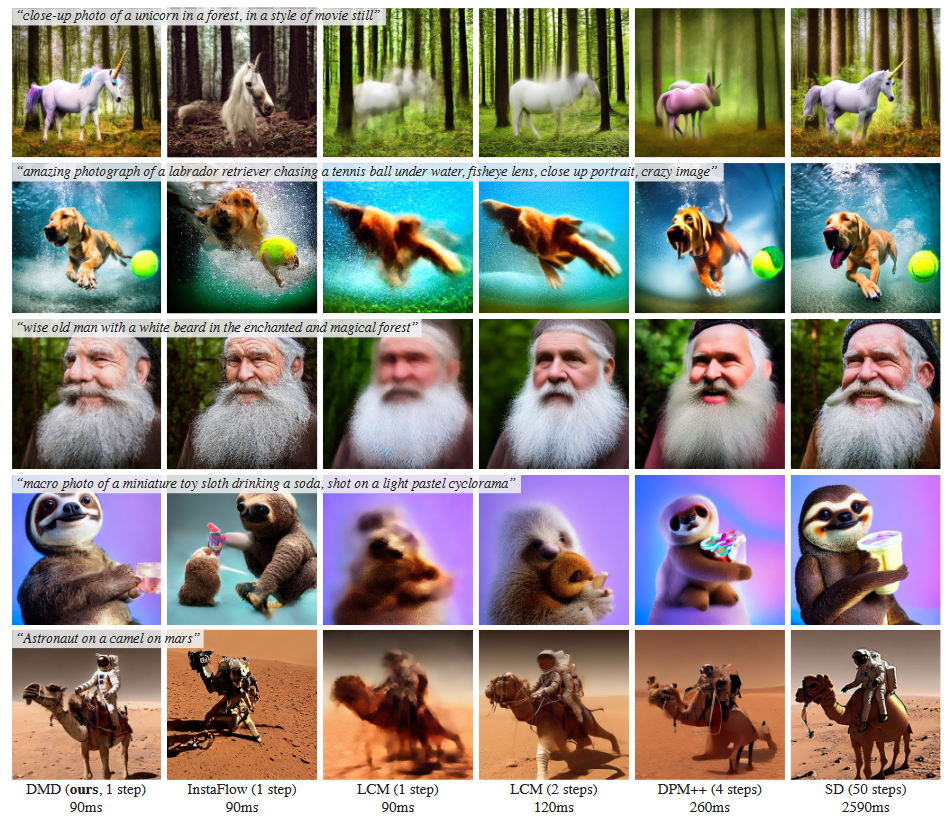
图6:从预训练的扩散模型(此处为稳定扩散(右))开始,分布匹配蒸馏算法生成的模型可以生成比之前的几步生成器(中)质量更高的图像(左),并且速度相同或更快。