一、介绍
扩散模型最近在图像生成和音频生成中产生了高质量的结果,并且在新的数据模态中验证扩散模型有很大的性能。在这项工作中,作者提出了使用扩散模型生成视频,无论是无条件的和有条件的设置。
作者表示基本上可以使用高斯扩散模型的标准公式来生成高质量的视频,除了简单的架构变化之外,几乎没有修改,以在深度学习加速器的内存限制内,容纳视频数据。使用3D U-Net扩散模型架构训练生成固定数量视频帧的模型,并通过使用新的条件生成方法自回归应用该模型来生成更长的视频。另外还展示了视频和图像建模目标联合训练的好处。并在视频预测和无条件视频生成上测试了该方法,实现了最先进的样本质量分数,并且还在文本条件视频生成上展示了有希望的第一个结果。
二、VDM
在图像建模的先前工作中,图像扩散模型中 \(\textcolor{blue}{\hat{x}_θ}\) 的标准架构是 U-Net,它的构造为空间下采样(Spatial downsampling),然后空间上采样(Spatial upsampling),其中在进行每一步空间上采样时都通过跳跃连接(skip connections)来对对应同一层的下采样所得到的特征图进行联系。该网络是由 2D 卷积残差块层(ResBlock)构建的,每个这样的卷积块后面都跟着一个空间注意力块(Spatial attention)。条件信息(例如 \(\textcolor{blue}{c}\) 和 \(\textcolor{blue}{λ_t}\))以添加到每个残差块中的嵌入向量的形式提供给网络。
如果要把U-Net扩展到视频领域,那么需要把里面的卷积全部替换成3D的来使用。但是如果直接使用3D卷积,其实计算的开销会十分的巨大。本来在像素空间训练图像生成任务的扩散模型已经会花费很多计算成本,而再加上3D卷积,就更不用说了。因此作者建议将图像扩散模型架构扩展到由固定数量帧的块给出的视频数据,使用特定类型的 3D U-Net,该网络在空间(Spatial)和时间(Temporal)上进行分解。
1️⃣具体而言,它们将每个 2D 卷积更改为space-only 3D 卷积,例如,由原来每个 3x3 卷积更改为 1x3x3 卷积(维度索引对应着视频帧,空间高度,宽度)。
2️⃣保留空间注意力块,并且每个空间注意力块中的注意力仍然是对空间的注意力;即,第一个轴被视为批处理轴。
3️⃣其次,在每个空间注意块之后,还插入了一个时间注意力块(Temporal attention),该时间注意力块对第一个轴执行注意并将空间轴视为批处理轴。并在每个时间注意力块中使用相对位置嵌入(relative position embeddings),以便网络可以以不需要视频时间的绝对概念的方式区分帧的顺序。VDM模型架构可视化如图 1 所示。
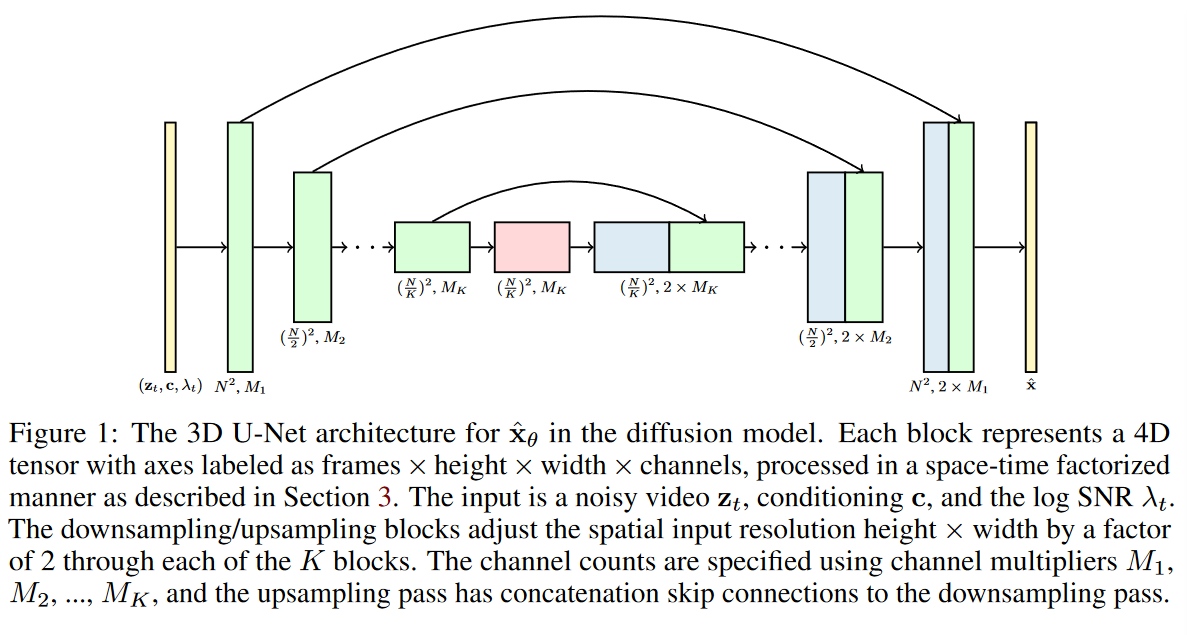
由于其计算效率,分解时空注意力的使用被认为是视频转换器的一个不错的选择。分解时空架构的一个优点是,将模型屏蔽为在独立图像而不是视频上运行特别简单,只需删除每个时间注意力块内的注意操作即可并修复注意力矩阵以在每个视频时间步精确匹配每个键和查询向量。这样做的好处是,它允许在视频和图像生成方面联合训练模型。作者在实验中发现这种联合训练对于样本质量很重要。
1.重构指导采样
论文的另一个主要创新是为无条件扩散模型提供了一种条件生成的方法。这种条件生成方法称为梯度条件法(gradient conditioning method),它修改了扩散模型的采样过程,使用基于梯度优化的方式来改善去噪数据的条件损失(conditioning loss),从而可以让生成的视频通过自回归地方式扩展至更长的时间步和更高的分辨率。由于梯度条件法中所使用的附加梯度项可以解释为一种额外的指导,而这种指导其实基于模型对条件数据的重建,因此论文将该方法称为重建引导采样(reconstruction-guided sampling),或简单地称为重建指导(reconstruction guidance)。
在训练的阶段,由于计算资源限制,往往只能在一个固定的帧数下面训练一个视频,而且这个帧数往往很短(比如论文中的16帧)。但是在采样(推理)阶段,我们可以先生成一个16帧的视频\(\textcolor{blue}{x^a \sim p_\theta(x)}\) ,然后在这个基础上拓展得到第二个视频\(\textcolor{blue}{x^b \sim p_\theta(x^b|x^a)}\) ,这样一来就可以通过自回归的方式拓展采样的视频到任意长度。但是这种采样方式需要我们显式地训练一个条件生成模型\(\textcolor{blue}{p_\theta(x^b|x^a)}\),或者通过插值的方式从无条件生成模型\(\textcolor{blue}{p_\theta(x)}\)近似得到。之前的工作通常都是通过“替换法”来进行自回归视频拓展,简单来说替换法就是对两条件样本进行联合训练\(\textcolor{blue}{p_\theta(x = [x^a,x^b])}\) ,但是在扩散模型前向的具体过程中\(\textcolor{blue}{x^b}\)对应的部分保持正常的迭代更替,而\(\textcolor{blue}{x^a}\)对应的部分被替换为一个固定的\(\textcolor{blue}{q(z_s^a|x^a)}\)或者\(\textcolor{blue}{q(z_s^a|x^a,z^a_t)}\),也就是始终需要参考\(\textcolor{blue}{x^a}\) 。 论文认为这种方式下\(\textcolor{blue}{x^b}\)对应的部分的更替仅仅是\(\textcolor{blue}{\hat{x}^b_\theta(z_t) \approx \mathbb{E}_q[x^b|z_t]}\) ,而真正理想的更替应该是\(\textcolor{blue}{\mathbb{E}_q[x^b|z_t,x_a]}\) , 这样才能够和上一个视频有更好的一致性。论文将上述更替方案改写为\(\textcolor{blue}{\mathbb{E}_q[x^b|z_t,x_a] = \mathbb{E}_q[x^b|z_t]+(\sigma^2_t/\alpha_t)\nabla_{z^b_t}\log q(x^a|z_t)}\) ,它使用基于梯度优化的方式来改善去噪数据的条件损失,提出的条件重构采样,其公式如下:
