一、PSNR 峰值信噪比
🐦用于衡量一张带有噪声的图片与干净的图片之间的差异。
计算方式:PSNR的计算方式涉及到均方误差(MSE):
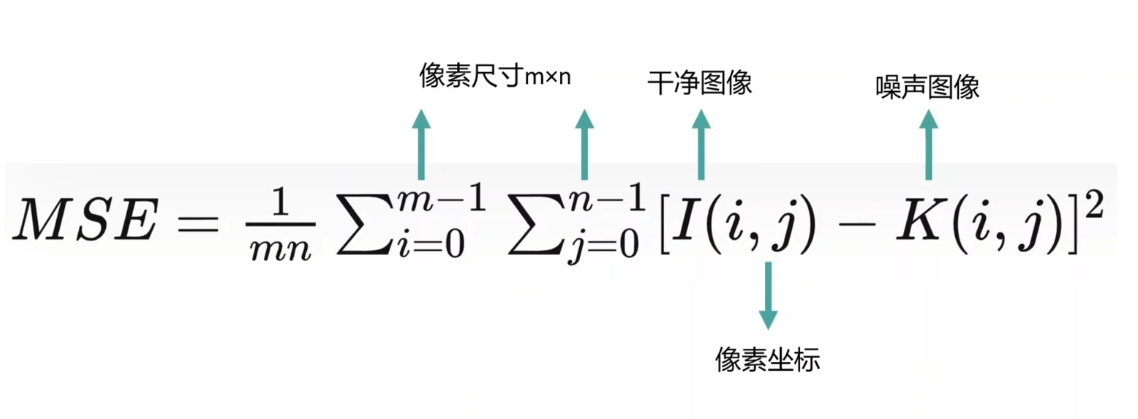
由此可以根据下式计算PSNR:
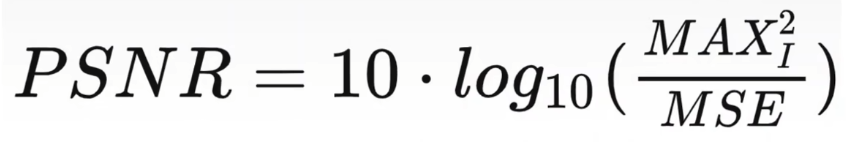
其中,MAX表示图片的动态范围:\(\textcolor{blue}{2^b-1}\),也就是可能的最大像素值。
两张图片差异越小,其中MSE就越小,PSNR就越大,这就意味着图像质量越好。
二、SSIM 结构相似性
🐦用于衡量图片的失真程度,也可以用于衡量两张图片之间的相似程度。
计算方式:SSIM衡量了图片三个性质,分别是亮度,对比度,结构。
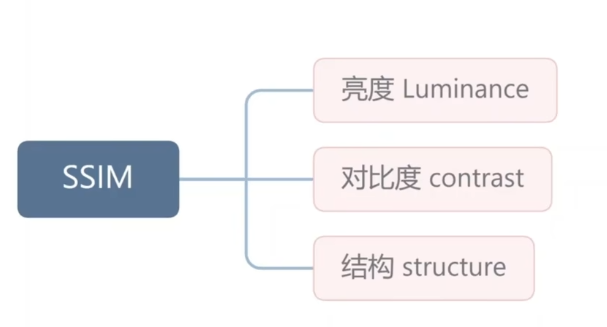
1️⃣其中,亮度指的是所有像素值灰度的平均值。
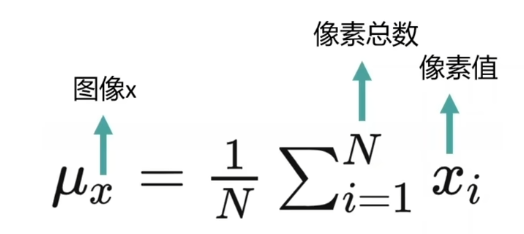
那么在分别计算好两张图片的亮度之后,可通过下面这个函数计算它们之间的亮度对比:
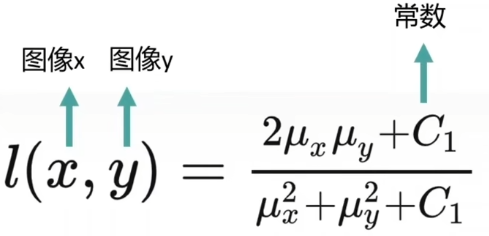
当且仅当\(\textcolor{blue}{\mu_x = \mu_y}\)时,\(\textcolor{blue}{l(x,y)}\)能取到最大值1,否则在0~1之间。
2️⃣对比度,是要计算灰度的标准差,所以图像x的标准差以及相应的对比函数,如下所示:

3️⃣结构对比,采用的是相关系数,用协方差除以方差的积来表示:

所以SSIM的最终表达式为:

同样的,当且仅当两个图像之间的亮度,对比度,结构都相同时,\(\textcolor{blue}{S(x,y)}\)能取到最大值1,否则在0~1之间。当我们取权重都为1时,SSIM就变成了:

其中,\(\textcolor{blue}{C_1 =(K_1 L)^2 ,K_1 = 0.01,L}\)为像素的动态范围,8位图像就是255。\(\textcolor{blue}{C_2 =(K_2 L)^2 ,K_2 = 0.03}\),\(\textcolor{blue}{C_3 =C_2/2}\)
在实际使用的时候,SSIM并不是直接对整张图像求平均以及方差,而是采用一个叫做圆对称的高斯加权公式。采用一个大小为11x11,标准差为1.5,和为1的高斯核,作为滑动窗口,求局部的均值,标准差和方差,最后对所有的局部SSIM求均值,得到MSSIM。
在引入高斯核之后,相应的均值,标准差,协方差公式也进行了相应的修改,权重采用高斯核的参数w:
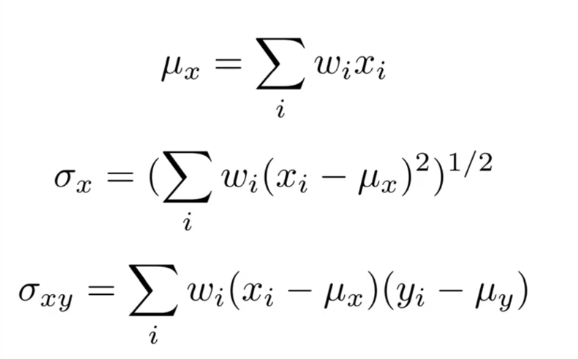
高斯核带来的一定程度上的模糊,是为了捕捉更高层的几何特征,而不是让比较仅仅停留在像素的尺度上。MSSIM确实不仅可以用来衡量两个图像之间的相似度,也可以用于当作损失去训练模型:

即图像越不相似,SSIMD的值就越接近为1,可以用作网络的损失函数。
MS-SSIM则进一步考虑了图像的多尺度信息。它通过在不同的尺度上计算SSIM。然后将这些SSIM值进行加权平均,得到最终的MS-SSIM值。这样可以更好地捕捉到图像的细节和结构信息。
三、LPIPS 学习感知图像块相似度
LPIPS也可以称作感知损失,用图像的深度特征来衡量两张图片的相似度。
来源于CVPR2018的一篇论文《The Unreasonable Effectiveness of Deep Features as a Perceptual Metric》。LPIPS 比传统方法(比如L2/PSNR, SSIM, FSIM)更符合人类的感知情况。LPIPS的值越低表示两张图像越相似,反之,则差异越大。
将左右的两个图像块和中间的图像块进行比较:

如图表示,每一组有三张图片,由传统的评价标准如L2、SSIM、PSNR等评价结果和人体认为的大不相同,这是传统方法的弊端。如果图片平滑,那么传统的评价方式则大概率会失效。而目前GAN尤其是VAE等生成模型生成结果都过于平滑。 而最后三行的评价为深度学习的方式,可以看到,通过神经网络(非监督、自监督、监督模型)提取特征的方式,并对特征差异进行计算能够有效进行评价,而且能够和人体评价相似。
LPIPS的具体计算流程:
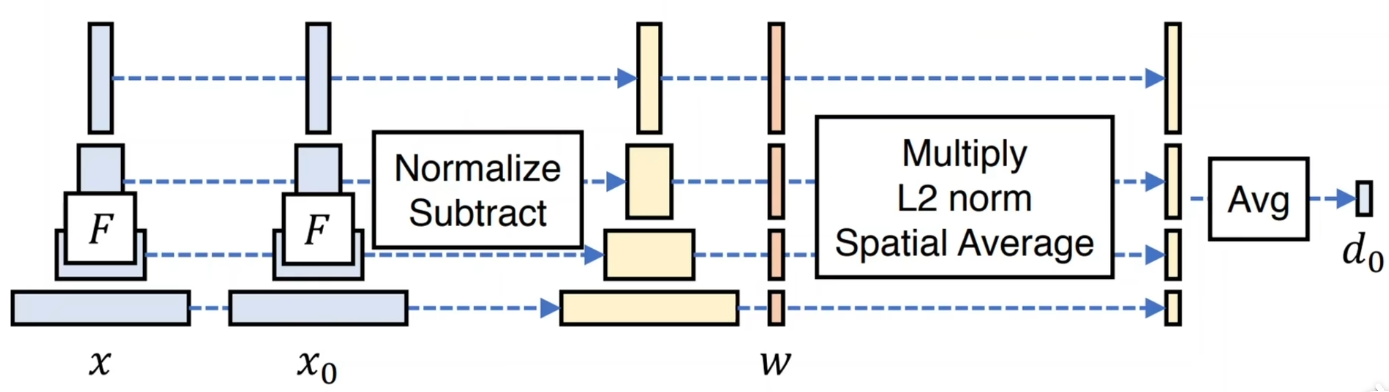
1️⃣把需要对比的图像\(\textcolor{blue}{x,x_0}\)输入到网络F当中,这个F可以是简单的VGG或者是Alexnet。
2️⃣把每一层经过激活函数的输出都拿出来进行Normalize归一化
3️⃣再经过w层给予一个权重,然后求两个网络各层特征向量之间的L2误差
4️⃣最后对所有层的误差取平均,得到相似度\(\textcolor{blue}{d_0}\),图像相似度越低,深度特征之间的差异就越大,LPIPS的输出结果就越大。
给定Ground Truth图像参照块\(\textcolor{blue}{x}\)和含噪声图像失真块\(\textcolor{blue}{x_0}\),感知相似度度量公式如下:

两个输入\(\textcolor{blue}{x,x_0}\)送入神经网络F(可以为VGG、Alexnet)中进行特征提取,对每个层的输出进行激活后归一化处理,记为\(\textcolor{blue}{\hat{y}^l,\hat{y}^l_0 \in R^{H_l\times W_l\times C_l}}\),然后经过w层权重\(\textcolor{blue}{w_l}\)点乘后计算L2距离,最后取平均获得距离。
四、FID
FID的计算是基于两个图像分布之间的特征向量空间的Fréchet的距离。FID的计算公式为:
\[\huge FID(P,G) = ||\mu_P - \mu_G||^2 + Tr(\Sigma_P + \Sigma_G - 2 * \sqrt{\Sigma_P\Sigma_G})\]
其中:
1️⃣\(\textcolor{blue}{P}\)表示真实图像分布的特征向量集合,通常使用Inception网络的中间层的输出来表示。
2️⃣\(\textcolor{blue}{G}\)表示生成图像分布的特征集合,也使用相同的方式表示。
3️⃣\(\textcolor{blue}{\mu_P}\)和\(\textcolor{blue}{\mu_G}\)分别是\(\textcolor{blue}{P}\)和\(\textcolor{blue}{G}\)的特征向量集合的均值。
4️⃣\(\textcolor{blue}{\Sigma_P}\)和\(\textcolor{blue}{\Sigma_G}\)分别是\(\textcolor{blue}{P}\)和\(\textcolor{blue}{G}\)的特征向量集合的协方差矩阵。
5️⃣\(\textcolor{blue}{Tr(\Sigma_P + \Sigma_G - 2 * \sqrt{\Sigma_P\Sigma_G})}\)表示协方差矩阵的迹的平方根