一、前言
扩散模型也被称为是分数模型,在图像生成、音频合成以及视频生成等领域都取得了前所未有的成功。但扩散模型依赖于迭代生成过程,该过程逐渐从随机初始向量中消除噪声。然而该过程往往都需要计算和样本质量的灵活权衡,因为使用额外的计算进行更多次迭代通常会产生质量更好的样本。然而,与 GAN、VAE或归一化流等单步生成模型相比,扩散模型的迭代生成过程通常需要 10-2000 倍的计算量来生成样本,这导致推理速度慢和实时应用受到限制。
而本次所介绍的一致性模型(Consistency Models)最大的特点就是具有实现高效的单步生成,而不牺牲迭代采样的重要优势。

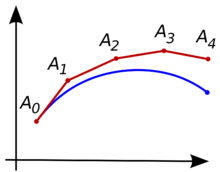
它是建立在连续时间扩散模型中的概率流 (PF) 常微分方程 (ODE) 之上,通过ODE我们能得到一条可以将数据分布平滑地转变为易于处理的噪声分布的轨迹,我们学习将 ODE 轨迹上的任何点(例如 \(\textcolor{blue}{x_t}\)、\(\textcolor{blue}{x_{t^\prime}}\) 和 \(\textcolor{blue}{x_T}\) )到其原点(例如 \(\textcolor{blue}{x_0}\))的映射。即从某个样本到某个噪声的加噪轨迹上的每一个点,都可以经过一个函数\(\textcolor{blue}{f}\)映射为这条轨迹的起点。由于模型的一个显着特性是:同一轨迹上的点映射到同一初始点。因此,作者将此类模型称为一致性模型。
一致性模型允许我们只需一次网络评估,就能通过转换随机噪声向量(ODE 轨迹的端点\(\textcolor{blue}{x_T}\) )来生成数据样本(ODE 轨迹的初始点\(\textcolor{blue}{x_0}\))。具体而言,从噪声中采样一个点,送入\(\textcolor{blue}{f}\)中,就得到了其对应的数据样本。这就是Consistency Models 的快速 one-step 生成,同时该模型仍然允许 few-step 采样,以权衡计算量和样本质量。它们还支持零样本(zero-shot)数据编辑,例如图像修复、着色和超分辨率生成。
在训练方面,研究团队为 Consistency Models 提供了两种基于自洽性的方法。第一种方法依赖于使用数值 ODE 求解器和预训练扩散模型来生成 PF ODE 轨迹上的相邻点对。通过最小化这些点对的模型输出之间的差异,该研究有效地将扩散模型蒸馏为 Consistency Models,从而允许通过 one network 评估生成高质量样本。
第二种方法则是完全消除了对预训练扩散模型的依赖,可独立训练 Consistency Models。这种方法将 Consistency Models 定位为一类独立的生成模型。
二、模型原理
1.SDE 以及 ODE
假设我们有数据分布\(\textcolor{blue}{p_{data}(x)}\),扩散模型通过如下的 SDE 形式对数据分布进行加噪:
\[\huge dx_t=\mu(x_t,t)dt+\sigma(t)dw_t-(1)\]
由宋飏博士推导出,上述 SDE 存在一个 ODE 形式的解轨迹:
\[\huge dx_t =[\mu(x_t,t)-\frac{1}{2}\sigma(t)^2\nabla \log p_t(x_t)]dt -(2)\]
其中,\(\textcolor{blue}{\nabla \log p(x)}\)作为\(\textcolor{blue}{p(x)}\)的得分函数。作者采用EDM的设置方法,令\(\textcolor{blue}{\mu(x_t,t) = 0}\),\(\textcolor{blue}{\sigma(t)=\sqrt{2t}}\),并训练一个分数模型\(\textcolor{blue}{s_\phi(x_t,t)}\)去拟合\(\textcolor{blue}{\nabla \log p_t(x)}\),则有\(\textcolor{blue}{s_\phi(x_t,t) \approx \nabla \log p_t(x)}\),然后将这些代入到式2,则能得到如下表达式:
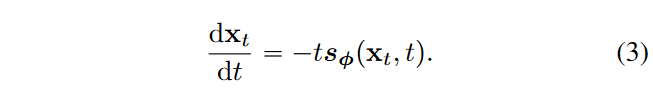
将该方程称之为empirical PF ODE。接下来,我们对\(\textcolor{blue}{\hat{x}_T \sim \pi=\mathcal{N}(0,T^2I)}\)进行采样,以初始化empirical PF ODE,并使用任何数值 ODE 求解器(例如 Euler 和 Heun 求解器 )对该式子进行求解,获得解轨迹\(\textcolor{blue}{\lbrace \hat{x}_t\rbrace_{t \in [0,T]}}\) 。该轨迹可看作高斯分布样本到数据分布样本的映射,由此产生的\(\textcolor{blue}{\hat{x}_0}\)可以被视为来自数据分布\(\textcolor{blue}{p_{data}(x)}\)的近似样本。
Euler:一种一阶数值方法,用以对给定初值的常微分方程求解,属于递归算法。该方法的思想就是用许多小的折线段去逼近曲线。
如该微分方程为例:\(\textcolor{blue}{y^\prime(t)=f(t,h(t)),y(t_0)=y_0}\)
希望用\(\textcolor{blue}{y}\)在点\(\textcolor{blue}{(t_0,y(t_0))}\)附近的线性近似来得到其近似解。利用\(\textcolor{blue}{t_n}\)时刻的数值,用单步欧拉方法,可得到时刻\(\textcolor{blue}{t_{n+1} =t_n+h}\)的近似值:
\[\huge y_{n+1} = y_n + hf(t_n,y_n)\]
欧拉方法的图示。待求的曲线为蓝色,它的折线近似为红色。
Heun被称为改进的欧拉方法。
如该微分方程为例:\(\textcolor{blue}{y^\prime(t)=f(t,h(t)),y(t_0)=y_0}\),并定义步长为\(\textcolor{blue}{h = t_{i+1} -t_i}\)
首先计算中间值:\(\textcolor{blue}{\hat{y}_{i+1} = y_i + hf(t_i,y_i)}\)
再计算下一个时刻的最终近似值:\(\textcolor{blue}{y_{i+1} = y_i + \frac{h}{2}(f(t_i,y_i)+f(t_{i+1},\hat{y}_{i+1}))}\)
特点:Heun是比Euler方法求解更加准确,并且收敛的速度比Euler还要快,但计算量比较高,会耗费更多的计算资源。
2. Consistency Models
有了PF ODE,我们已经能做到采样一个高斯噪声,然后通过求解ODE,映射到数据。但求解ODE仍然是一个迭代过程,要计算很多次\(\textcolor{blue}{s_\theta(x_t,t)}\),效率很低。而Consistency Models要做的就是直接学习这个ODE表示的映射,也就是它的解任给某个轨迹上的点\(\textcolor{blue}{(x_t,t)}\) ,一步inference得到\(\textcolor{blue}{(x_0)}\)
定义:给定一条解轨迹\(\textcolor{blue}{\lbrace x_t\rbrace_{t \in [\epsilon,T]}}\),定义一致性函数为:
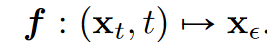
对于这条轨迹上的任意点\(\textcolor{blue}{(x_t,t)}\) ,一致性函数都能将它们映射到相同的一个值,即:

并且对于轨迹的起点\(\textcolor{blue}{x_0 = x_\epsilon}\) ,(其中\(\textcolor{blue}{\epsilon}\)是一个小正数(如0.002),这里引入\(\textcolor{blue}{\epsilon}\)是为了避免在\(\textcolor{blue}{t=0}\)处易出现的数值不稳定。)则我们有
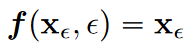
那么对于轨迹中任意一点,我们代入先验分布, 即可得到\(\textcolor{blue}{f(x_T,T)=x_\epsilon}\)。这样也就完成了一步采样
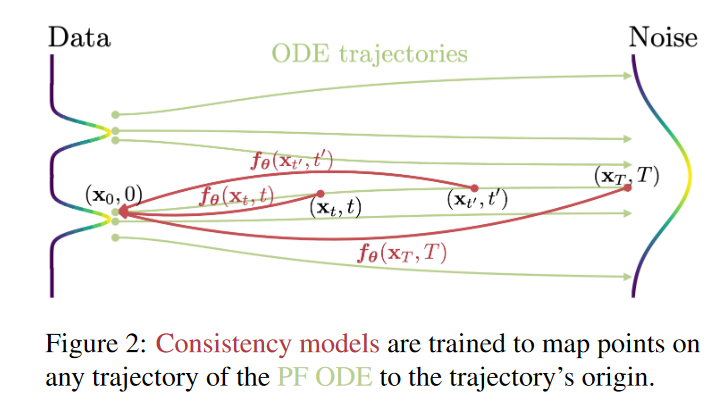
由此,我们可以训练一个神经网络来拟合 \(\textcolor{blue}{f}\),但是网络要满足一致性函数的两个最关键特性:
1️⃣\(\textcolor{blue}{f(x_\epsilon,\epsilon)=x_\epsilon}\)
2️⃣任意\(\textcolor{blue}{t_1,t_2\in [\epsilon,T]}\)满足\(\textcolor{blue}{f(x_{t_1},t_1)=f(x_{t_2},t_2)}\)
也就是说,即要保证\(\textcolor{blue}{f(x_\epsilon,\epsilon)=x_\epsilon}\)是恒等函数,也要保证轨迹上的任意两点输出值一致。将此约束称为边界条件,所有一致性模型都必须满足这个边界条件,如果无法保证轨迹上的任意点映射到起点的输出值相同,自然也无法保证一致性模型能够单步生成正确样本,因此它对于一致性模型的成功训练起着至关重要的作用。作者给出了两种实现此边界条件的方法。
假设有一个自由形式的深度神经网络\(\textcolor{blue}{F_\theta(x,t)}\) ,其输出与\(\textcolor{blue}{x}\)具有相同的维度。第一种方法是简单地将一致性模型参数化为:

第二种方法是使用跳跃连接来参数化一致性模型,即:

其中\(\textcolor{blue}{c_{skip}(t),c_{out}(t)}\)都是可微函数,当\(\textcolor{blue}{c_{skip}(\epsilon)=1,c_{out}(\epsilon)=0}\),就可以天然实现\(\textcolor{blue}{f(x_\epsilon,\epsilon)=x_\epsilon}\)。由于第二种方法与许多扩散模型非常相似,使得更容易借用强大的扩散模型架构来构建一致性模型。因此,在所有实验中都遵循第二个参数化。之后的第二个性质通过训练目标去拟合。
单步采样:当我们训练好一个一致性模型\(\textcolor{blue}{f_\theta(x_t,t)}\)时,其生成过程,就是从先验分布采样一个随机样本\(\textcolor{blue}{\hat{x}_T \sim \mathcal{N}(0,T^2I)}\),代入到模型当中进行评估,一步到位\(\textcolor{blue}{\hat{x}_\epsilon = f_\theta(\hat{x}_T,T)}\)。
多步采样:显然,\(\textcolor{blue}{f(x_T,T)=x_\epsilon}\)可以得到我们想要的生成结果。但一般认为,这样的生成误差会比较大。就像DDPM也可以通过预测噪声直接从\(\textcolor{blue}{x_t}\)预测\(\textcolor{blue}{x_0}\),但我们会依赖\(\textcolor{blue}{x_t,x_0}\)预测\(\textcolor{blue}{x_{t-1}}\)的依次向下采样来获得\(\textcolor{blue}{x_0}\)来减小误差。同样的。一致性模型也能够每次从\(\textcolor{blue}{x_{\tau_n}}\)预测出初始的\(\textcolor{blue}{x}\)后,回退一步来预测\(\textcolor{blue}{x_{\tau_{n-1}}}\)。通过这种交替去噪和噪声注入步骤方式来多次评估一致性模型,就能减小误差,提高样本质量。

具体的伪代码如下所示:

3. 训练方式
3.1 通过蒸馏训练一致性模型(CD)
1️⃣该方法的前提是,我们已经拥有了一个训练好的分数模型\(\textcolor{blue}{s_\phi(x_t,t)}\),那么就可以根据PF ODE\(\textcolor{blue}{\frac{dx_t}{dt}=-ts_\phi(x_t,t)}\)去构建一条确定性的解轨迹\(\textcolor{blue}{\lbrace x_t\rbrace_{t \in [\epsilon,T]}}\)。依据上述方法,训练\(\textcolor{blue}{f_\theta(x_t,t)}\)在其轨迹上到\(\textcolor{blue}{\hat{x}_\epsilon}\)的映射,直接优化\(\textcolor{blue}{||f_\theta(x_t,t)-\hat{x}_\epsilon||^2_2}\)。但这可能需要我们监督该轨迹上的每一个点的模型输出都一致,即都能有\(\textcolor{blue}{f_\theta(x_t,t)=\hat{x}_\epsilon}\)。这个效率就很低了。一种最简单的办法是直接监督一条轨迹上相邻两个点的模型输出一致。
2️⃣此时假设采样轨迹的时间序列为:\(\textcolor{blue}{\epsilon = t_1 < t_2 < ...<t_N=T}\),其中\(\textcolor{blue}{t_i =(\epsilon^{\frac{1}{\rho}}+\frac{i-1}{N-1(T^{\frac{1}{\rho}}-\epsilon^{\frac{1}{\rho}})})^\rho,\rho=7}\),当\(\textcolor{blue}{N}\)足够大的时候,我们可以通过运行数值 ODE 求解器的一个离散化步骤。
3️⃣然后采样出该轨迹上两个相邻的点\(\textcolor{blue}{t_{n+1}}\)以及\(\textcolor{blue}{t_{n}}\)的样本。先采样得到\(\textcolor{blue}{x_{t_{n+1}}}\),再利用Euler方法一阶近似估计\(\textcolor{blue}{x_{t_{n}}}\)。这个估计,我们表示为\(\textcolor{blue}{\hat{x}^\phi_{t_{n}}}\) ,定义为

其中,\(\textcolor{blue}{\Phi(...;\phi)}\)表示应用于经验 PF ODE 的单步 ODE 求解器的更新函数。例如当使用Euler求解器时,\(\textcolor{blue}{\Phi(x,t;\phi)=-ts_\phi(x,t)}\),代入到式6则有:

首先,我们可以根据\(\textcolor{blue}{dx_t=\mu(x_t,t)dt+\sigma(t)dw_t}\),将高斯噪声添加到数据\(\textcolor{blue}{x}\)上,从\(\textcolor{blue}{\mathcal{N}(x,t^2_{n+1}I)}\)的中采样\(\textcolor{blue}{x_{t_{n+1}}}\),然后利用公式6数值ODE求解器的一个离散化步骤来计算\(\textcolor{blue}{\hat{x}^\phi_{t_{n}}}\),就能够生成相邻数据点\(\textcolor{blue}{(\hat{x}^\phi_{t_{n}},x_{t_{n+1}})}\)在 PF ODE 轨迹上。然后。通过最小化\(\textcolor{blue}{(\hat{x}^\phi_{t_{n}},x_{t_{n+1}})}\)对的输出差异来训练一致性模型,因而有如下训练损失:
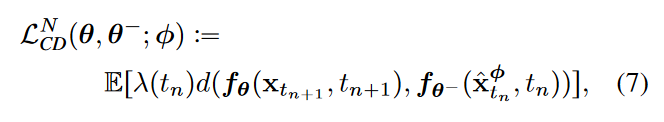
其中,\(\textcolor{blue}{\lambda(\cdot)}\)是权重,论文实验发现\(\textcolor{blue}{\lambda(\cdot)\equiv 1}\)效果最好,\(\textcolor{blue}{d(\cdot,\cdot)}\)是度量函数,可以是L1, L2或者LPIPS等等。
L1:\(\textcolor{blue}{d(x,y)=||x-y||_1}\)
L2:\(\textcolor{blue}{d(x,y)=||x-y||_2^2}\)
LPIPS:\(\textcolor{blue}{d(x,x_0)=\sum\limits_{l}\frac{1}{H_lW_l}\sum\limits_{h,w}||w_l\bigodot (\hat{y}^l_{hw}-\hat{y}^l_{0hw})||_2^2}\)
这里很重要的一个特别之处是\(\textcolor{blue}{\theta^-}\)是参数\(\textcolor{blue}{\theta}\)在训练过程中的指数移动平均,在实践中,通过模型参数\(\textcolor{blue}{\theta}\)的随机梯度下降来最小化目标,同时使用指数移动平均值 (EMA) 更新\(\textcolor{blue}{\theta^-}\)。也就是说,给定衰减速率\(\textcolor{blue}{0\leq \mu <1}\),在每个优化步骤后执行以下更新:

指数移动平均(EMA):是将每次梯度更新后的权值和前一次的权重进行联系,使得本次更新收到上次权值的影响。其公式就是:\(\textcolor{blue}{v_t = \alpha \cdot v_{t-1} + (1-\alpha)\cdot \theta_t}\),\(\textcolor{blue}{\alpha}\)代表衰减速率,用于控制模型的更新速度,一般设为0.9-0.999。\(\textcolor{blue}{\theta_t}\):在第\(\textcolor{blue}{t}\)次更新得到的所有参数权重。\(\textcolor{blue}{v_t}\):在第\(\textcolor{blue}{t}\)次更新的所有参数移动平均数。普通的参数权重相当于一直累积更新整个训练过程的梯度,使用EMA的参数权重相当于使用训练过程梯度的加权平均(刚开始的梯度权值很小)。由于刚开始训练不稳定,得到的梯度给更小的权值更为合理,所以EMA会有效。
算法 2 总结了整个训练过程。将\(\textcolor{blue}{f_{\theta^-}}\)称为“目标网络”,将 \(\textcolor{blue}{f_{\theta}}\) 称为“在线网络”。作者发现,与简单设置\(\textcolor{blue}{\theta^-,\theta}\)相比,公式8中的 EMA 更新和stopgrad算子可以极大地稳定训练过程,提高一致性模型的最终性能。

3.2 从数据中直接训练一致性模型(CT)
本文还提供了第二种训练方法:可以在不依赖任何预先训练的扩散模型的情况下训练一致性模型。由于在CD的方法中,需要预训练好的分数模型\(\textcolor{blue}{s_\phi(x_t,t)}\)去逼近真实的分数函数\(\textcolor{blue}{\nabla \log p_t(x)}\)。当我们没有预训练的模型时,就需要从数据中去估计\(\textcolor{blue}{\nabla \log p_t(x)}\)。对于论文中的SDE,可以推导出估计\(\textcolor{blue}{\nabla \log p_t(x)}\)的公式:


其中,\(\textcolor{blue}{x \sim p_{data}}\)并且\(\textcolor{blue}{x_t \sim \mathcal{N}(x;t^2I)}\)。
利用该式子,作者构建了新的consistency training (CT) loss记作\(\textcolor{blue}{\mathcal{L}^N_{CT}(\theta,\theta^-)}\)
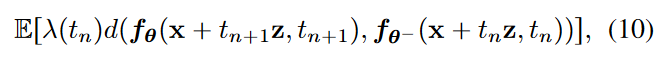
作者证明了,在\(\textcolor{blue}{N \rightarrow \infty}\)的极限内,当使用Euler方法作为ODE求解器时,对\(\textcolor{blue}{\nabla \log p_t(x)}\)的估计足以取代预训练的扩散模型,即\(\textcolor{blue}{s_\phi(x,t) \equiv \nabla \log p_t(x)}\),就有:
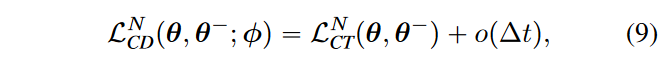
当\(\textcolor{blue}{N \rightarrow \infty}\),即\(\textcolor{blue}{Δt \rightarrow 0}\),那么就可以省去后面这一项\(\textcolor{blue}{o(Δt)}\),两个方法的目标函数相等。为了提高实际性能,作者建议根据调度函数\(\textcolor{blue}{N(\cdot)}\)在训练期间逐步增加 N。当N很小(即\(\textcolor{blue}{Δt}\)很大),这有利于训练开始时更快的收敛。相反,当 N 较大(即\(\textcolor{blue}{Δt}\)较小)时,它训练速度收敛较慢,但生成样本的质量会提高。作者为了获得最佳性能,还发现 μ 应根据调度函数\(\textcolor{blue}{\mu(\cdot)}\)随 N 一起变化。算法3提供了一致性训练的完整算法:

三、实验
本文均使用一致性蒸馏(CD)和一致性训CTCT)来学习真实图像数据集上的一致性模型。数据集:包括 CIFAR-10、ImageNet 64x64、LSUN Bedroom 256x256 和 LSUN猫 256x256。评估指标包括:FID(越低越好)、Inception Score(越高越好)、Precise(越高越好)和 Recall(越高越好)。
1.训练一致性模型
作者首先在 CIFAR-10 上进行了一系列实验,为了解各种超参数对分别通过CD和CT两种方法进行训练的一致性模型性能的影响。如下图3所示:
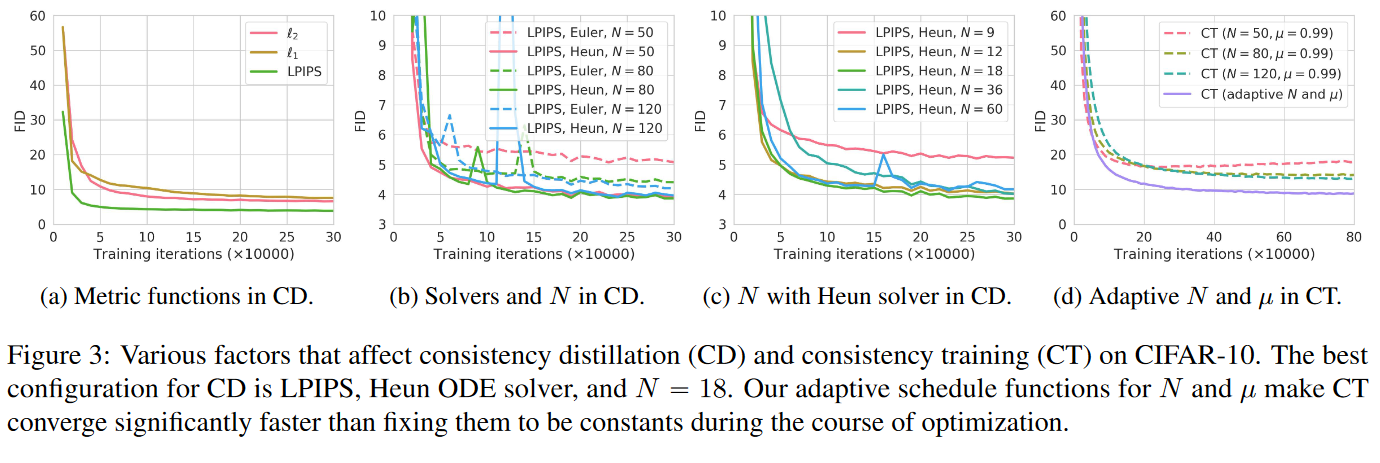
图a:CD 的最佳指标是 LPIPS,它在所有训练迭代中都大幅优于 \(l_1\) 和 \(l_2\)。
图b:CD的最佳求解器是Heun ODE求解器。此外,在 N 相同的情况下,Heun 的二阶求解器一直都优于 Euler 的一阶求解器。这证实了定理 1,即在相同的 N 下,由高阶 ODE 求解器训练的最优一致性模型具有更小的估计误差。
图c:在使用相同的训练损失以及ODE求解器,CD表现最好的指标是离散化步骤为N=18的时候。一旦N足够大,CD的性能就变得对N不敏感。
图d:CT的收敛对N高度敏感——较小的N会导致更快的收敛速度,但样本质量较差,而较大的N会导致较慢的收敛速度,但收敛后的样本质量会更好。这与我们在第 3.2 节中的分析相匹配,并促使我们实际选择逐渐增加 CT 的 N 和 μ,以平衡收敛速度和样本质量之间的权衡。如图3d所示,N和μ的自适应调度显着提高了CT的收敛速度和样本质量。
2.Few-Step 图像生成
2.1 蒸馏
在当前文献中,与一致性蒸馏(CD)最直接可比的方法是渐进式蒸馏(PD);作者在 CIFAR-10、ImageNet 64x64 和 LSUN 256x256 上对 PD 和 CD 进行全面比较,所有结果如图 4 所示。

渐进式蒸馏(PD),它是由斯坦福大学和谷歌的研究者在论文《On Distillation of Guided Diffusion Models》中提出使用两步蒸馏(two-step distillation)方法来提升无分类器指导的采样效率。在第一步中,他们引入单一学生模型来匹配两个教师扩散模型的组合输出;在第二步中,他们利用提出的方法逐渐地将从第一步学得的模型蒸馏为更少步骤的模型。
在所有采样迭代中,与PD原始论文中的平方 l2 距离相比,使用 LPIPS 度量均匀地提高了 PD。随着采取更多采样步骤,PD 和 CD 都会得到改善。并且在所有数据集、采样步骤和所考虑的度量函数中,CD 均优于 PD,但 Bedroom 256x256 上的单步生成除外,其中使用 l2 的 CD 略低于使用 l2 的 PD。
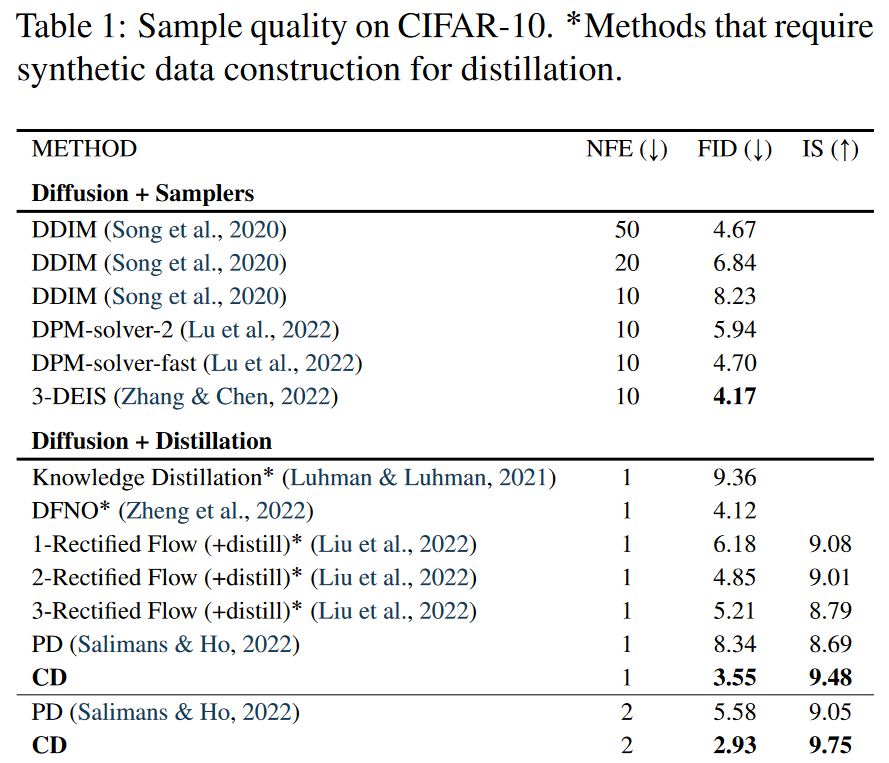
迄今为止,这两种方法都是在蒸馏之前不构建合成数据的蒸馏方法。与此形成鲜明对比的是,其他蒸馏技术,例如知识蒸馏和DFNO,必须通过从扩散模型生成大量样本来准备大型合成数据集,这些样本具有昂贵的数值ODE/SDE 求解器。如表 1 所示,CD 甚至优于需要合成数据集构建的蒸馏方法,例如知识蒸馏和 DFNO。
2.2 直接生成
在表 1 和表 2 中,作者将直接训练一致性模型 (CT) 的样本质量与使用一步生成和两步生成的其他生成模型进行了比较。

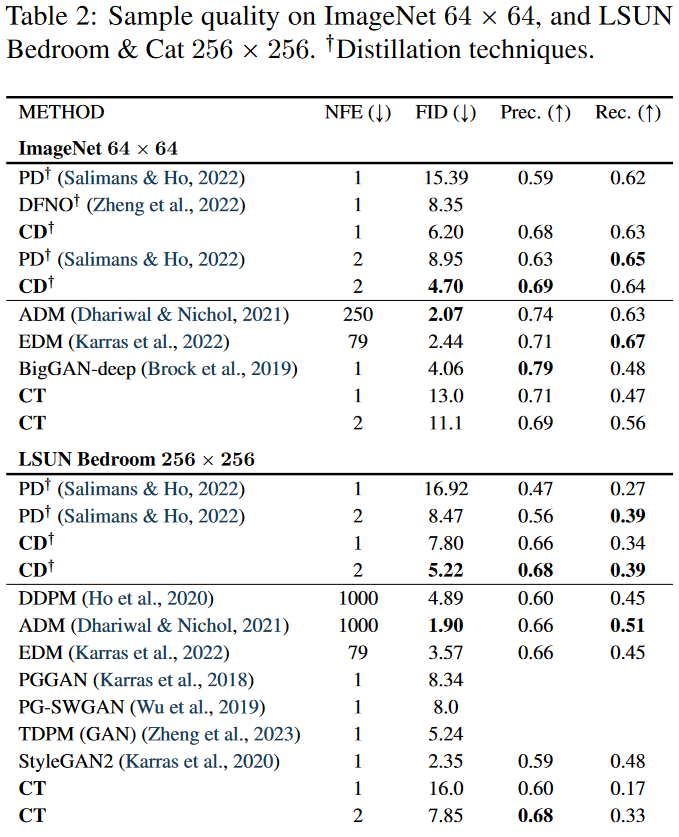
效果上,目前diffusion > CD > diffusion distillation > CT,(GAN的效果不太好比较,在有些数据集上,经过这么多年充分调教的GAN性能甚至再次反超diffusion,有的数据集上则不如CT)。作为单步方法的CD和CT打不过diffusion,其实可以理解,一方面这one-one mapping本身非常复杂,还是比较难拟合的;另一方面,consistency models训练方法是约束一条ODE轨迹上的相邻点输出相同,模型拟合不好的话,每一步的误差都会累积下来。
在图 5 中,我们提供了 EDM 样本(顶部)、单步 CT 样本(中)和两步 CT 样本(底部)。下面图像都是从同一初始噪声向量获得的,我们可以发现这些样本都具有显着的结构相似性,即使 CT 和 EDM 模型是彼此独立训练的。

四、总结
本文介绍了一致性模型,这是一种专门为支持一步和少步生成而设计的生成模型。凭经验证明,一致性蒸馏方法(CD)在多个图像基准和小采样迭代上优于扩散模型的现有蒸馏技术。此外,作为独立的生成模型,一致性模型比除 GAN 之外的现有单步生成模型生成更好的样本。与扩散模型类似,它们还允许零样本图像编辑应用程序,例如修复、着色、超分辨率、去噪、插值和笔画引导图像生成。不过consistency model才刚刚提出不久,在训练方法上还有很多待研究的技术。而作为一种单步生成方法,相对于diffusion在性能上有着显著优势。想必后面会跟进很多改进方法。