一、前言
在之前Classifier Guidance的博客当中提到了关于Classifier Guidance的几个问题:
- 仅针对带标签的数据集;
- 该分类器需要对所有 noise 都有分类能力,所以还不能直接加载常见的预训练模型,该分类器的质量可能会影响按类别生成的效果;
- 当我们的分类器训练的还不足够好的时候,采用该分类器关于其输入的梯度可以在输入空间中产生任意(甚至是对抗)的方向,生成图像可能会通过人眼不可察觉的细节欺骗分类器,实际上并没有按条件生成。
为了解决这些问题,本篇作者提出了Classifier-Free Guidance(无分类器指导)方案,该方案完全避免了任何分类器,直接训练带类别信息的噪声预测模型来实现特定类别图片的生成。此外,Classifier-Free方法不局限于类别信息的融入,它还能实现将语义信息(文本)融入到diffusion model中,实现更为灵活的文生图。这用Classifier Guidance是很难做到的。目前的很多工作如DALLE,Stable Diffusion, Imagen等都是Classifier-Free形式。下面就具体看看它是如何去实现的:
二、原理
1.具体方案
Classifier-Free Diffusion的实现非常简单,它就是直接定义:
\[\huge p_\theta(x_{t-1}|x_t,y)=\mathcal{N}(x_{t-1};\mu_\theta(x_t,y),\sigma^2_tI)\]
\(\textcolor{blue}{\mu_\theta(x_t,y)}\)一般参数化为:
\[\huge \mu_\theta(x_t,y)=\frac{1}{\sqrt\alpha_t}(x_t-\frac{\beta_t}{\sqrt{1-\bar{\alpha}_t}}\epsilon_\theta(x_t,y,t))\]
训练损失就是:
\[\huge E_{x_0,y \backsim \tilde{p}(x_0,y),\epsilon \backsim \mathcal{N}(0,I)}[||\epsilon-\epsilon_\theta(x_t,y,t)||^2]\]
Classifier-Free方案也模仿Classifier-Guidance方案加入了\(\textcolor{blue}{s}\)参数的缩放机制来平衡相关性与多样性。那么我们就能将原本Classifier Guidance的更新后的均值\(\textcolor{blue}{μ(x_t)+σ^2_ts∇_{x_t}\log p(y|x_t)}\)改写成:
\[\Large μ(x_t)+σ^2_ts∇_{x_t}\log p(y|x_t)=s[μ(x_t)+σ^2_t∇_{x_t}\log p(y|x_t)]-(s-1)\mu(x_t)\]
Classifier-Free方案相当于直接用模型拟合了\(\textcolor{blue}{μ(x_t)+σ^2_t∇_{x_t}\log p(y|x_t)}\),我们进一步化简再引入\(\textcolor{blue}{w=s−1}\)参数,可以得到:
\[\huge \hat\epsilon_\theta(x_t,y,t) = (1+w)\epsilon_\theta(x_t,y,t)-w\epsilon_\theta(x_t,t)\]
用上式代替\(\textcolor{blue}{ϵ_θ(x_t,y,t)}\)来做生成。那无条件的\(\textcolor{blue}{ϵ_θ(x_t,t)}\)怎么来呢?作者通过新引入一个特定的输入\(\textcolor{blue}{ϕ}\),它对应的目标图像为全体图像,加到了模型的训练中,这样我们就可以认为\(\textcolor{blue}{ϵ_θ(x_t,t)=ϵ_θ(x_t,ϕ,t)}\)。
也就是说,使用无分类器引导的最终解析式要求我们只需要训练两个模型,其中一个通过\(\textcolor{blue}{\epsilon_\theta(x_t,t)}\)训练是无条件生成模型(例如常规的 DDPM),另一个通过\(\textcolor{blue}{\epsilon_\theta(x_t,y,t)}\)训练基于条件生成模型。而我们甚至可以使用同一个模型同时训练表示两者,区别只在于无条件生成时将条件信息置为空序列\(\textcolor{blue}{ϕ}\)。
实际训练的时候会通过一个概率\(\textcolor{blue}{p_{uncond}}\)随机去掉条件(\(\textcolor{blue}{y}\)换成\(\textcolor{blue}{ϕ}\)),从而达到分别训练有条件以及无条件模型。这样做的好处是使得联合训练很容易实现,且不会使得训练过程变得复杂。
注:在GLIDE等其他文章中其公式也可以这样表示:\(\hat\epsilon_\theta(x_t,y,t) =\epsilon_\theta(x_t,t)+ s(\epsilon_\theta(x_t,y,t)-\epsilon_\theta(x_t,t))\)
guidance scale在0时候是unconditional,1时候是普通conditional,>1是完全conditional,当condition的信息少的时候可以调高scale>1获得更单一的结果,但condition的信息太多时候可以拉低scale<1获得更多样且质量更高的结果。
怎么实现无条件以及有条件一起训练?以一定的概率(通常为10-20%)将标签替换为”[]”
1 | def get_uncond_tokens_mask(tokenizer: Encoder): |
训练以及采样:

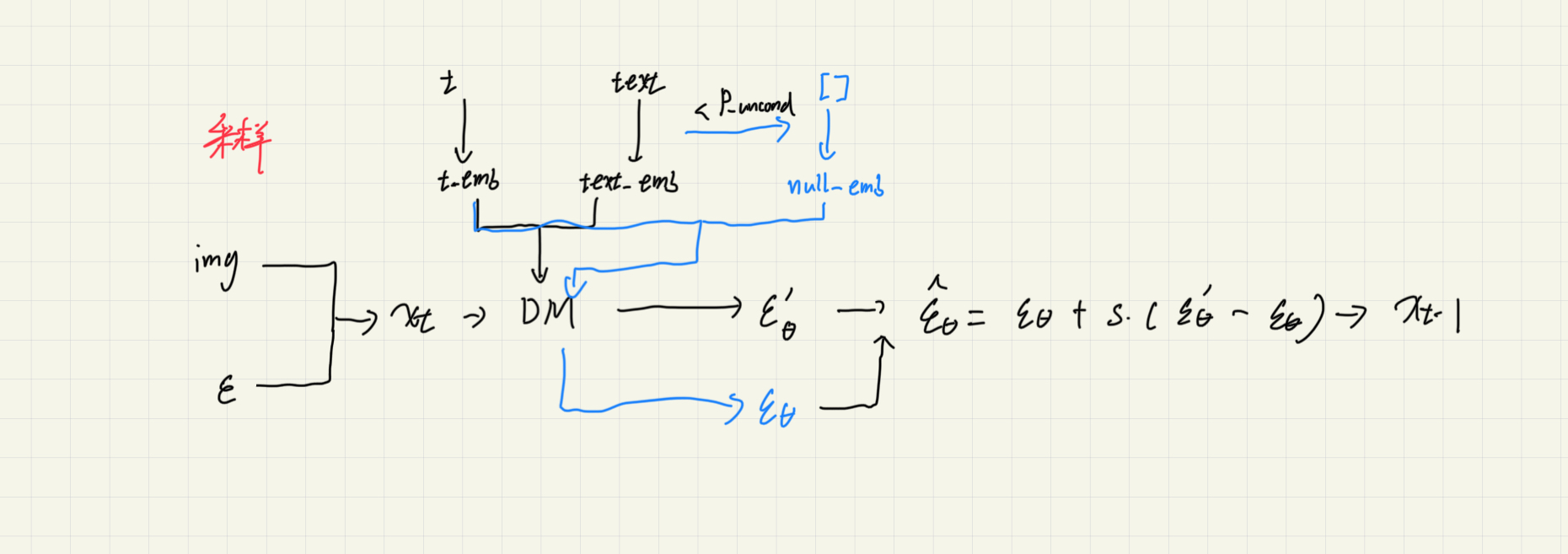
我们可以通过下面的表格对比普通的diffusion model,classifier-guided与classifier-free三种方式的差异。
| 模型 | 训练目标 | 实现功能 | 训练数据 |
|---|---|---|---|
| DM(DDPM,DDIM) | \(\epsilon_\theta(x_t,t)\) | 从服从高斯分布的噪声中生成图片 | 图片 |
| classifier-guided DM | \(\epsilon_\theta(x_t,t)\)和分类器\(p(y|x_t)\) | 从服从高斯分布的噪声中生成特定类别的图片 | DM:图片 分类器:噪声图片-标签对 |
| classifier-free DM | \(\epsilon_\theta(x_t,t),\epsilon_\theta(x_t,y,t)\) | 从服从高斯分布的噪声中生成符合文本描述的图片 | 图片-文本对 |
classifier-free DM将类别信息(或语义信息)集成到diffusion model的训练过程中,训练\(\textcolor{blue}{\epsilon_\theta(x_t,t),\epsilon_\theta(x_t,y,t)}\)。训练的过程中也会加入无类别信息(或语义信息)的图片进行训练。
三、实验
该实验分别在ImageNet 64x64和128x128进行训练,采用与ADM相同的模型框架和超参数,而作者也表明实验的目的是为了证明在无分类指导能够实现类似于有分类器指导的FID/IS的权衡,并不一定要使得样本质量到达SOTA。
1.对比实验
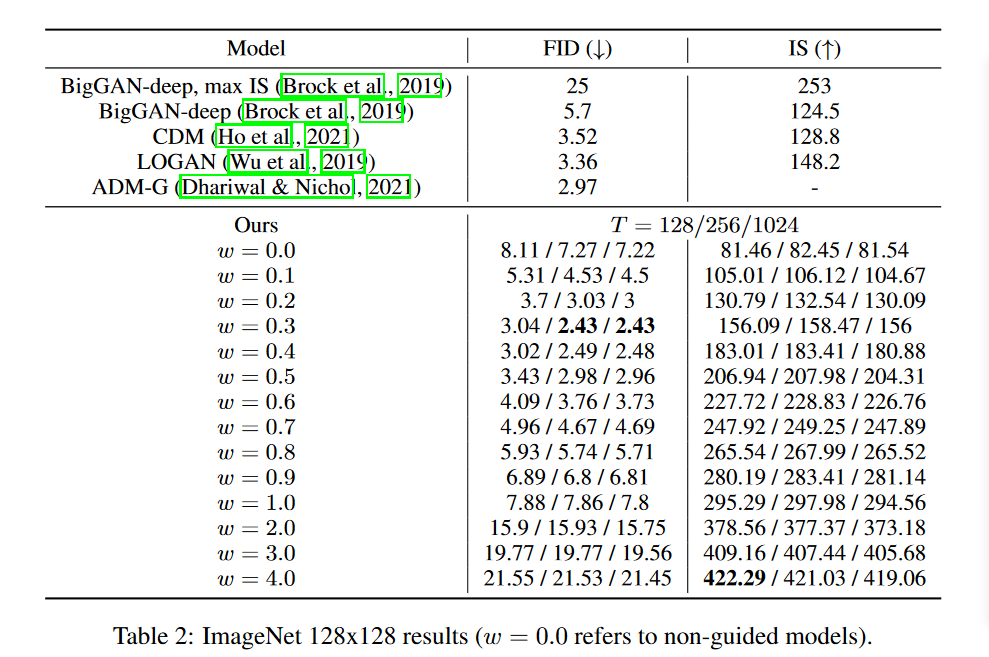
由实验结果可以发现,作者提出的模型通过少量指导(w = 0.1 或 w = 0.3,具体取决于数据集)获得了最佳 FID 结果,并通过强指导(w ≥ 4)获得了最佳 IS 结果。在这两个极端之间,我们看到这两个感知质量指标之间存在明显的权衡,FID 随着 w 单调递减,IS 随着 w 单调递增。

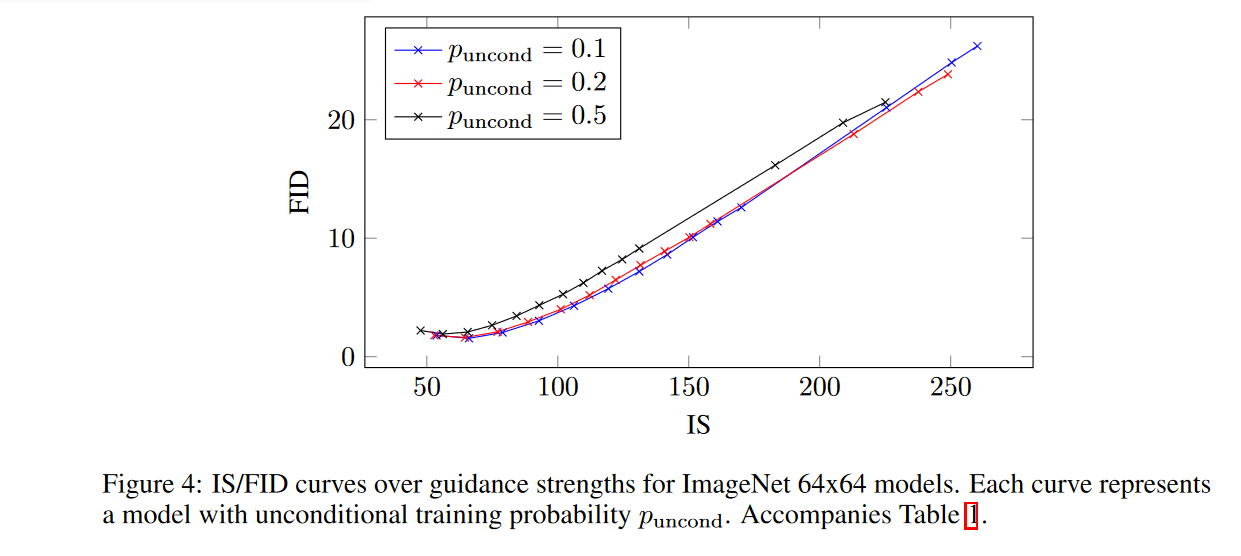
2.无条件训练的概率\(p_{uncond}\)的影响
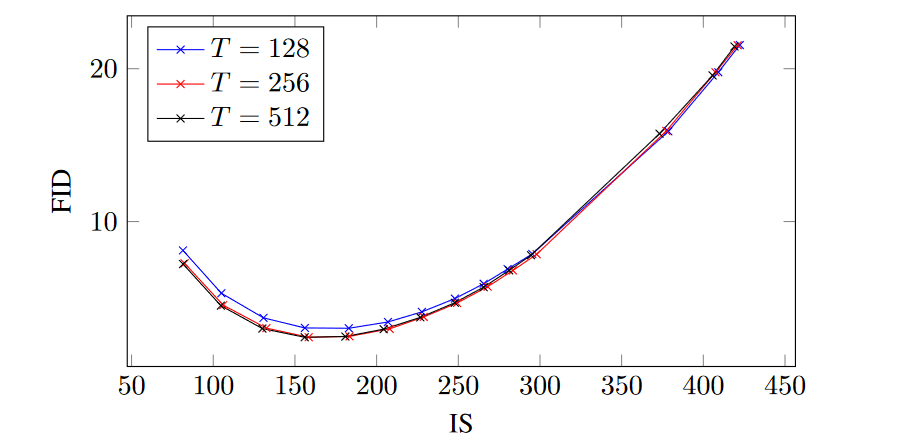
3.采样步数的影响
采样步骤数 T 对扩散模型的样本质量有重大影响,因此作者在这里研究不同 T 对模型的影响。在一定引导强度范围内改变 \(T \in [128, 256, 512]\)。正如预期的那样,当 T 增加时,样本质量会提高,对于该模型,T = 256 在样本质量和采样速度之间取得了良好的平衡。
4.生成样本展示


四、Classifier guidance与Classifier-Free guidance的区别
第一点:无分类器指导方法最实际的优点是:只需在训练期间(随机删除条件)和采样期间(混合条件和无条件分数估计)对代码进行一行更改即可。相比之下,分类器指导使训练流程变得复杂,因为它需要训练额外的分类器。该分类器必须在噪声\(x_t\)上进行训练,因此不可能插入标准的预训练分类器。
第二点:由于无分类器指导能够像分类器指导一样权衡 IS 和 FID,而无需额外训练的分类器并且能够精细的控制。此外,Classifier-Free由无约束神经网络参数化,与分类器梯度不同。无分类器引导采样器遵循的步骤方向不类似于分类器梯度,因此不能被解释为对分类器的基于梯度的对抗性攻击。
第三点:无分类器引导的一个潜在缺点是采样速度。一般来说,分类器可以比生成模型更小、更快,因此分类器引导采样可能比无分类器引导更快,因为后者需要端到端训练两个模型,训练成本较大。而Classifier Guidance可以直接复用一个SOTA级别的扩散模型可以实现低成本控制生成。
五、总结
作者提出了无分类器指导,这是一种在扩散模型中提高样本质量同时降低样本多样性的方法。无分类器指导不需要额外训练分类器,只需要联合训练两个模型。实验的结果显示了无分类器指导的有效性,证实纯生成扩散模型能够最大化基于分类器的样本质量指标,同时完全避免分类器梯度。
六、其他
1、无分类器指导造成图像过饱和的原因分析
先从结果来看,如下图所示,当随着w的提高,图像的饱和度越高:

原因分析:图像的饱和度增加随着w提高而提高。而w是为了控制条件信息指导的程度。
\[\huge \hat\epsilon_\theta(x_t,y,t) = (1+w)\epsilon_\theta(x_t,y,t)-w\epsilon_\theta(x_t,t)\]
由上式可以进一步推出\(x_{t-1}\)分布下的均值和方差分别为:
\[\huge \hat\mu = \mu + w(\mu-\mu_\phi) \]
\[\huge \hat\sigma^2 = (1+w)^2\sigma^2+w^2\sigma^2_\phi\]
均值以及方差都发生了偏移,并且在同一分布下,是随着w的提高逐渐增加的,通过T步骤逐步扩散这些统计偏移量也逐渐累积。在数字图像处理中,过大的方差会往往表现出的图像的对比度提高,从而导致图像过度饱和。
