一、前言
本文章出自《Diffusion Models Beat GANs on Image Synthesis》
如何评价生成模型的质量:1)真实性 ,2)多样性。
图像质量的衡量指标通常为 FID,Inception Score 和 Precision,然而这些指标无法体现多样性。目前 GANs 在大部分的图像生成任务上都取得 SOTA 成绩,GANs 在生成多样性方面比 likelihood-based models 弱,另外 GANs通常比较难训练,如果没有选择合适的超参或正则很容易 collapsing 。
基于GANs的缺陷,有很多的工作在改进 likelihood-based models ,希望提高图像生成质量,然而和 GANs 相比仍有差距,另外生成样本的速度比较慢。
Diffusions models 属于 likelihood-based models,其具有分布覆盖广,使用静态训练目标和易于扩展的优点,并且能够生成相当高质量图像,当前已在 CIFAR-10 上取得了 SOTA 成绩,然而在 LSUN 和 ImageNet 数据集上与 GANs 相比仍有差距。通过IDDPM的改进,扩散模型虽然已经可以在ImageNet数据集256×256 数据集上也可以生成高质量的样本。但是在FID分数上仍然比不上BigGAN-deep。
文章认为造成上述差距的原因为:
- GANs 的网络架构已经十分完善了;
- GANs 可以在多样性和逼真度方面取得平衡,虽可以产生高质量图像,但是不能覆盖整个分布。
基于此,本文想要改进现有 diffusion 模型架构,同时提出了可以平衡图像生成多样性和逼真度的方案。
1、评判生成样本的质量指标
1)IS指标
Inception Score (IS) 是衡量模型捕获完整 ImageNet 类分布的程度,同时仍然生成作为单个类的令人信服的示例的单个样本。IS是直接对生成图像进行评估,指标值越大越好。实际上其实就是算生成分布与真实发布的KL散度。
2)FID指标
FID 提供了Inception-V3用于潜在空间中生成样本分布和真实数据分布之间距离的差异。
在计算FID指标时,首先从真实数据分布和生成样本分布中抽取一组样本,然后使用预训练的Inception网络从这些样本中提取特征向量。接下来计算两个分布的均值和协方差矩阵,并计算它们之间的Frechet距离,得到FID值,该值越小表明生成样本分布越接近真实数据分布。

3) Improved Precision and 召回率
改进的精度(Precision):测量样本保真度作为模型生成的样本落入数据流形(数据分布)的比例(精度)。召回率:测量多样性作为数据样本落入样本流形(生成分布)的比例(召回率)。
关于流形的解释:流形是几何中的一个概念,我们观察到的数据是三维的,但其本质是一个二维流形,流形能够刻画数据的本质。高维数据其实是由低维流形生成的。如果我们能模拟这个生成过程,再通过对低维流形的微调,应该能得到对应的“有意义且有道理”的高维数据。
本篇论文的作者使用 FID 作为比较整体样本质量的默认指标,因为它是多样性和保真度的权衡,使用 Precision 或 IS 来衡量保真度,并使用 Recall 来衡量多样性或分布覆盖范围。
二、改进架构
原扩散模型DDPM中使用的是UNet架构作为去噪网络,而作者想要根据一下几点的架构改进,做消融实验,看是否能够提高图像生成质量。
增加深度(神经网络层数)并减小宽度(通道数),但保持模型尺寸相对恒定。
增加注意力头的数量。
在 32×32、16×16 和 8×8 分辨率下使用注意力,而不仅仅是在 16×16 下。
使用 BigGAN 的残差块进行上采样和下采样。
对残差连接使用\(1/\sqrt{2}\)因子缩放。
上述改进的比较是基于在ImageNet 128×128上训练模型,批量大小(batch_size)为 256,并使用 250 个采样步骤(timesteps)进行采样,使用FID指标进行比较。如表1所示:

在图 2 中观察到,虽然增加的深度有助于提高性能,但它会增加训练时间,并且需要更长的时间才能达到与更广泛的模型相同的性能。

作者还研究了其他更适合 Transformer 架构的注意力配置。为此,他们尝试使用更多的 heads 或者每个 head 使用更少的 channels。对于架构的其余部分,作者使用 128 个基本通道、每个分辨率 2 个残差块、多分辨率(multi-resolution)注意力和 BigGAN 上/下采样,并训练模型进行 700K 次迭代。表 2 显示了我们的结果,表明每个头使用更少的通道可以改善 FID。

根据图2右图,可以看出当我们每个头使用64通道时更有助于节省训练时间。
最后总结出作者采用的Unet架构为 128 个channels、每个分辨率下2个残差块、多分辨率(multi-resolution)注意力和 BigGAN 上/下采样,每个注意力头采用64通道。
1、自适应归一化
AdaGN,它在组标准化(GN)操作之后将时间步长t和类嵌入合并到每个残差块中,简单来说就是将组归一化后的值和条件做一个反射变换。
\[\huge AdaGN(h,y)=y_sGrounpNorm(h)+y_b\]
其中,h是第一个卷积后的残差块的激活函数,\(y = [y_s, y_b]\)是从timesteps和class embedding的线性投影获得的。
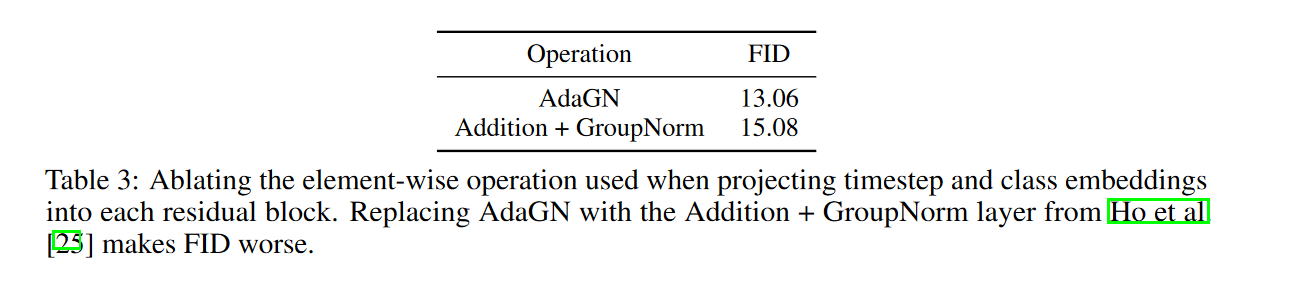
其中,Addition+GroupNorm指的是将h和\(y_s,y_b\)加起来后再做GroupNorm。
三、分类器指导(classifier-guidance)
这是一个利用图片类别标签指导图像生成的方案。给定了一个训练好的无条件扩散模型,使用分类器的梯度来调节预训练的扩散模型。作者在噪声图像\(x_t\)上训练分类器 \(p_\phi(y|x_t, t)\),然后使用梯度 \(∇_{x_t}\log p_\phi(y|x_t,t)\)引导扩散采样过程朝向任意类标签 y。如下,将进一步介绍这个是如何去实现的:
注:不管是无条件的扩散模型还是有条件的扩散模型,都可以使用分类器指导
1、条件扩散过程
首先作者定义了一个条件扩散过程\(\hat{q}\)类似于DDPM的扩散过程q,并假设$(y|x_0) $是每个样本的已知且容易获得的标签分布。就是默认了我们输入的每一张图片都有已知的对应类别。
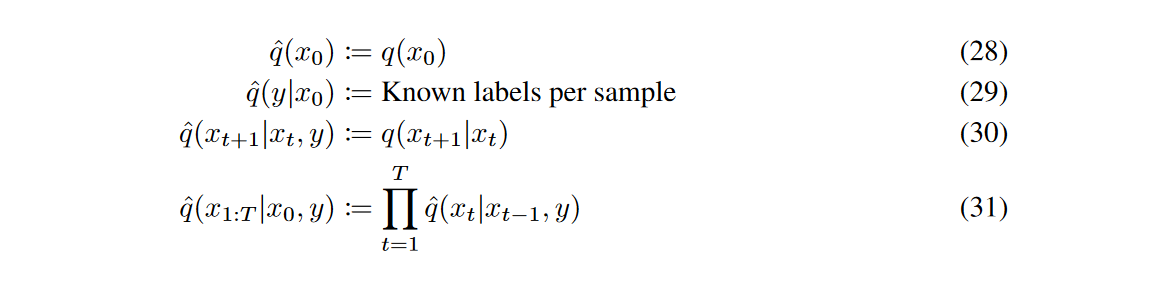
上述定义了以y为条件的扩散过程\(\hat{q}\),之后作者证明了在不以y为条件的情况下,\(\hat{q}\)加噪过程与q一致,分别证明了\(\hat{q}\)的边缘分布、条件分布以及联合分布:

按照类似的逻辑,可以进一步推出联合分布\(\hat{q}(x_{1:T} |x_0)\):

最后,还可以推导出\(\hat{q}(x_t)\)的边缘分布:
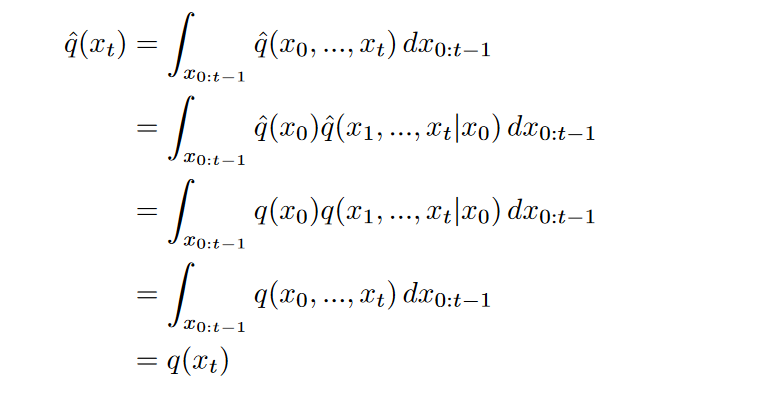
2、条件逆向过程
上述证明了,不管前向是否以y为条件,\(\hat{q}\)都与q前向过程的表现一致,说白了噪声不会对分类有帮助。接下来就是去推导条件逆向过程的解析形式。作者先是做了如下证明,该证明说明:\(\hat{q}(y|x_t)\)的分布只与当前时刻的\(x_t\),后一步\(x_{t+1}\)不影响该分布,为之后推导条件逆过程做了一个铺垫:
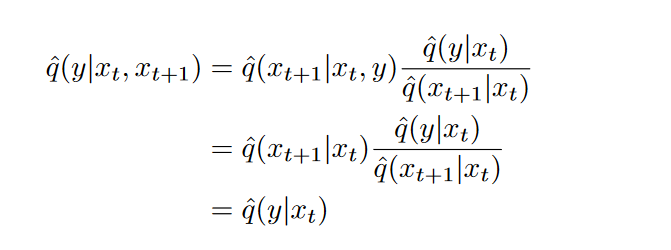
我们将带类别信息的去噪过程定义为\(\hat{q}(x_t|x_{t+1},y)\),由此我们就可以推导出条件逆过程:

在上述的逆过程当中,我们已知的量有label y 和\(x_{t+1}\)所以,\(\hat{q}(y|x_{t+1})\)其实是一个已知的常数(视为Z),因为它不依赖与未知变量\(x_t\)。然后我们希望从分布\(\hat{q}(x_t|x_{t+1},y)= Zq(x_t|x_{t+1})\hat{q}(y|x_t)\) 中采样\(x_t\)。然而我们也有了\(q(x_t|x_{t+1})\) 的神经网络近似值,称为 \(p_θ(x_t|x_{t+1})\),所以剩下的就是\(q(y|x_t)\)的近似值。于是我们可以根据\(x_t,y\)对再训练一个分类器\(p_\phi(y|x_t)\)去近似 \(q(y|x_t)\),我们就有了以下式子:

我们现在知道了带条件y的扩散模型的加噪以及去噪过程的分布或者公式的形式,接下来我们需要求\(p_{θ,\phi}(x_t|x_{t+1},y)\)的目标函数的形式,在DDPM我们是对其进行负对数似然。
我们知道的是 \(p_θ(x_t|x_{t+1})\)在DDPM中是用于拟合高斯分布的
\[\huge p_\theta(x_t|x_{t-1})=\mathcal{N}(\mu,Σ)=\frac{1}{\sqrt{2\piΣ}}\exp(-\frac{(x-\mu)^2}{2Σ})\]
对其取对数,可以进一步得到:
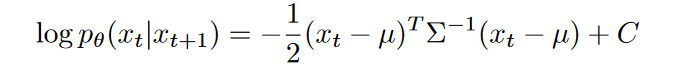
在无限扩散步数下,\(p_θ(x_t|x_{t+1})\)的方差足够小,作者假设 \(\log_ϕ p(y|x_t)\)相比\(Σ^−1\)有着更低的曲率,意思就是\(\log p_\phi(y|x_t)\)二阶展开式的曲率小于\(Σ^−1\),也就是二阶导数更小,因此只展开到一阶。然后再对\(\log p_ϕ(y|x_t)\)在 \(x_t=μ\)处进行泰勒展开:
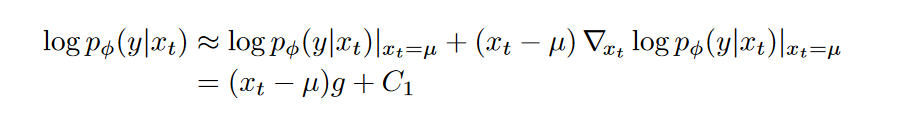
这里,\(g = ∇_{x_t} log p_φ(y|x_t)|_{x_t=μ}\),并且C1是常数。最后我们可以求出\(p_{θ,\phi}(x_t|x_{t+1},y)\)的一个对数似然:

其中,C4是推导过程当中一系列的一个归一化常数,最后把两个高斯分布的对数似然用了一个新的高斯分布\(p(z)\)去表示。

算法1为DDPM的算法流程,我们从扩散模型当中预测出\(x_t\)的均值和方差之后,要对均值做一个偏移。其偏移量(\(\Sigma g\)就是由分类器算出来的一个梯度乘以协方差),scale可以理解为条件指导的程度。
\[\huge x_{t-1}=\mu+s\Sigma∇_{x_t}logp_\phi(y|x_t)|_{x_t=\mu}+\Sigma \epsilon\]

由上述一系列推导我们可以得到一个结论:我们直接复用训练好的无条件扩散模型(因为前向过程表现出的效果是一致的),用一个分类器来调整生成过程就能实现控制生成。可以看到classifier求的是对 \(x_t\) 的梯度与Unet是没有关系。这个梯度信息的含义是:让 \(x_t\) 预测为 y 的概率更大的一个方向。classifier guided采样过程将这个梯度信息传递给\(x_{t-1}\)使得生成的图片不断朝期望类别靠近。
3、在DDIM中的条件采样
经过上述条件采样的推导,我们得到了均值的修正项\(s\Sigma∇_{x_t}logp_\phi(y|x_t)\),该修正项有一个特点,就是当\(\Sigma\)为0时,修正项也等于0,修正就失效了。
那么生成过程的方差可以等于0吗?然而DDIM,就是方差为0的生成过程。
原论文的DDIM就是特指\(σ_t=0\)的情形,其中“I”的含义就是“Implicit”,意思这是一个隐式的概率模型,此时从给定的\(x_T=z\)出发,得到的生成结果\(x_0\)是不带随机性的,因此采样过程中不涉及任何随机因素,最终生成图片将由一开始输入的图片噪声\(x_t\)所在分布的均值决定。我还做了以下实验用同一个\(x_t\)分别用DDIM和DDPM,各自进行两次采样:

因此这个上述的条件采样推导仅适用于随机扩散采样过程,不能应用于像 DDIM 这样的确定性采样方法。为此,作者使用改编自 Song 等人的基于分数的调节技巧。 它利用了扩散模型和分数匹配之间的联系。直接利用无条件模型预测的\(\epsilon_θ(x_t)\)等价于\(∇_{x_t}\log p_\phi(y|x_t)\):

然后可以将其代入 \(p(x_t)p(y|x_t)\) 的分数函数(梯度)中:
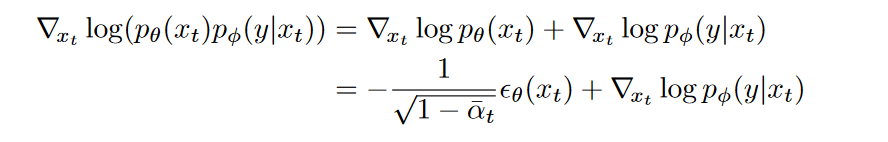
最后,我们可以定义一个新的\(\epsilon\)预测\(\hat{x}_t\):
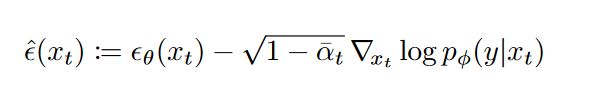
然后,我们可以使用与常规 DDIM 完全相同的采样过程,但使用修改后的噪声预测 \(\hat{\epsilon}_θ(x_t)\) 而不是\(\epsilon_θ(x_t)\)。这就意味着,不管生成方差是多少,我们只需要用\(ϵ_θ(x_t,t)−\sqrt{1-\bar{\alpha}_t}∇_{x_t}\log p_\phi(y|x)\)代替\(ϵ_θ(x_t,t)\)就可以实现条件控制生成了。算法2总结了相应的采样算法:

4、缩放(scale)分类器梯度
classifier的训练与扩散模型的训练可以是独立的。在训练classifier的时候可以使用噪声预测模型(Unet)的encoder部分作为主干,在后面接了一个分类层。但是classifier需要在\(x_t\)上进行训练。
在使用无条件 ImageNet 模型的初始实验中,作者发现常数因子(s)scale Classifier gradients的作用。当s=1,大约能保证生成的图片50%是想要的类别,随着s的增大,这个比例也能够增加。当s>1时,结果将会提高生成结果与输入标签y的相关性,但是会相应地降低生成结果的多样性,当s=10时,分类器的类别概率增加到接近 100%。图 3 显示出了这种效果。

图 3:来自无条件扩散模型的样本,带有分类器指导,以“彭布罗克威尔士柯基犬”类别为条件。使用分类器尺度s=1.0(左FID:33.0),而分类器尺度s=10.0(右;FID:12.0)会产生更多类一致的图像。
缩放 classifier gradients 的影响:
\[\huge s \cdot \nabla_x logp(y|x)= \nabla_x log \frac{1}{z}p(y|x)^s\]
式中,Z为常数,当 \(s>1\) ,分布\(p(y∣x)^s\)比 \(p(y∣x)\)更加陡峭,对于这个分布让它在概率密度更大的地方有更大的峰值,预测的结果会接近one-hot分布。所以使用大的scale会让模型更加关注 classifier ,从而产生更加逼真(多样性减少)的样本。
在上面的推导中,我们假设基础扩散模型是无条件的,对 \(p(x)\)进行建模,也还可以训练条件扩散模型\(p(x|y)\),并以完全相同的方式使用分类器指导。表4表明,通过分类器引导,无条件模型和条件模型的样本质量都可以得到极大的提高,我们可以看到,在足够高的规模下,引导无条件模型(guided unconditional model)可以非常接近无引导条件模型(unguided conditional model)的 FID。
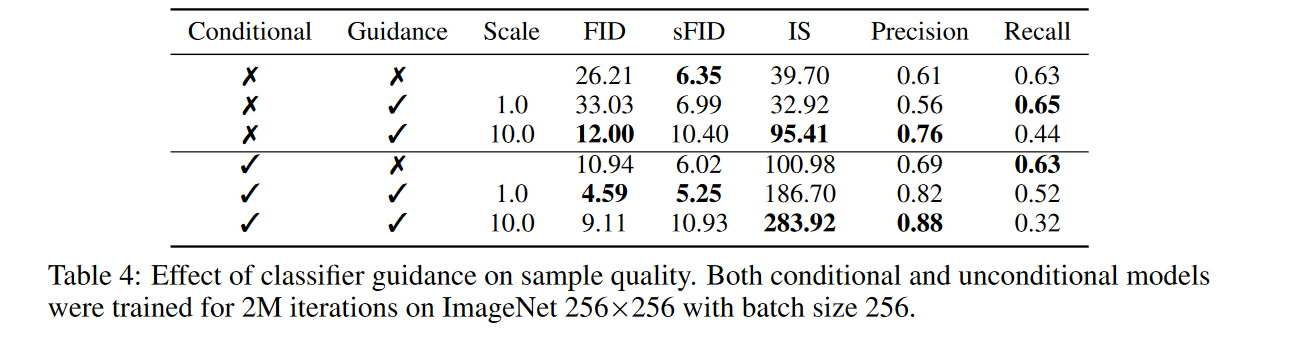
表4还表明了分类器指导(Classifier guidance)以Recall为代价提高了Precision,从而在样本保真度与多样性之间进行权衡,在图4中可以看到这种权衡是如何随梯度尺度变化的:

作者进一步对使用 guidance 的 diffusion 模型 和 BigGAN进行比较,发现2点现象:
- classifier guidance 在平衡 FID 和 IS 方面远优于 BigGAN;
- classifier guidance 在达到一个 precision 阈值后,就无法取得更好的 precision。

作者也提到了关于Classifier guidance的局限:
- 分类器指导技术目前仅限于标记数据集;
- 需要额外训练一个噪声版本的图像分类器,那么该分类器的质量会影响按类别生成的效果;
- 当我们的分类器训练的还不足够好的时候,采用该分类器关于其输入的梯度可以在输入空间中产生任意(甚至是对抗)的方向,采样出来的图像骗过了一个并不健壮的分类器并不代表我们确实逼近了条件分布。
四、实验结果
作者评估改进的模型架构在无条件图像生成的性能使用数据集 LSUN(分别对于类别bedroom, horse 和 cat),评估 classifier guidance 性能使用数据集 ImageNet (分辨率分别为 128×128, 256×256 和 512×512),几乎在每个任务上 diffusion models 都取得了 SOTA成绩。
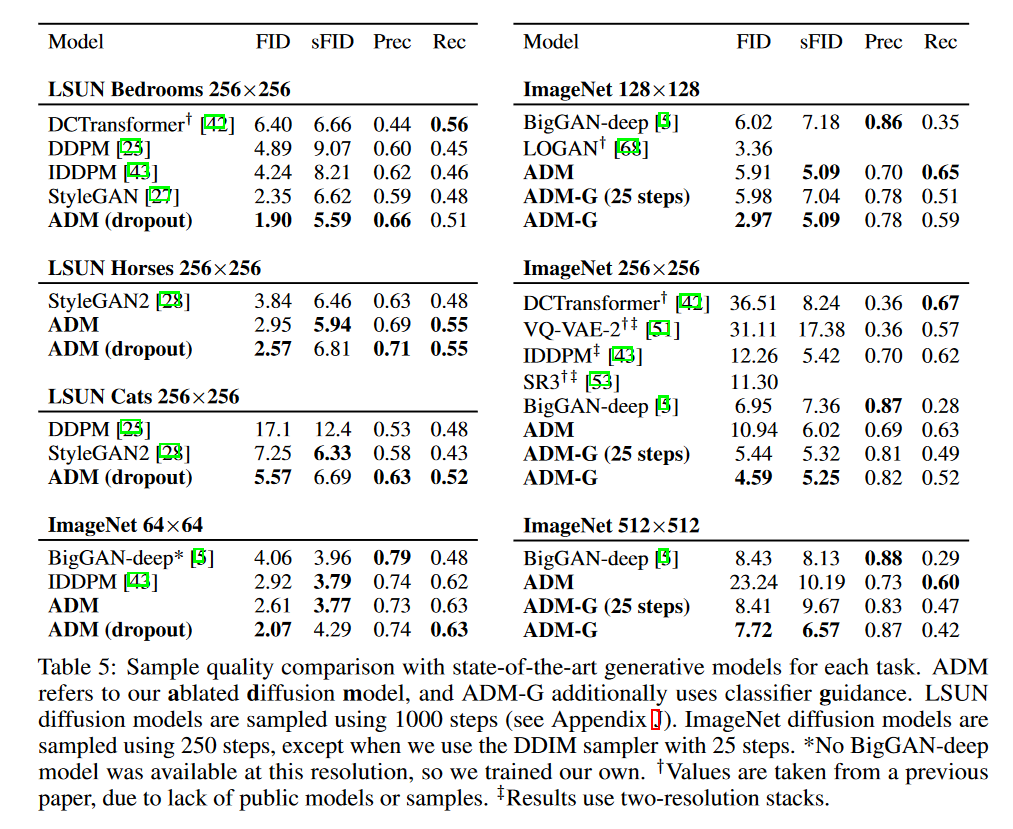
图 6 比较了最佳 BigGAN 深度模型和最佳扩散模型的随机样本。

1、与上采样方法进行比较
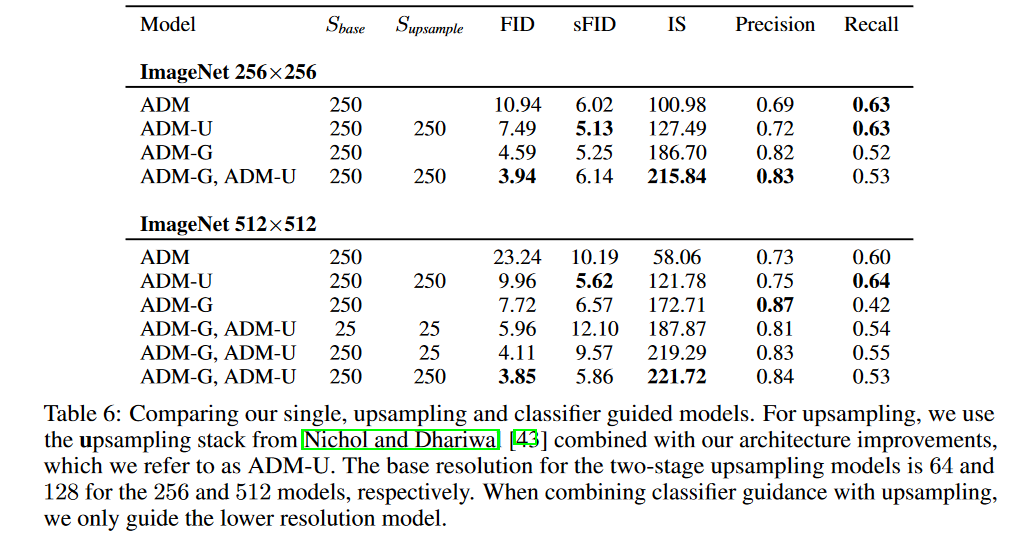
作者比较了使用两阶段采样的思想,通过将低分辨率扩散模型与相应的上采样扩散模型相结合来训练两阶段扩散模型。在表 6 中,表明引导和上采样可以提高不同轴上的样本质量。虽然上采样在保持高召回率的同时提高了精度,但指导提供了一个在多样性和更高的精度之间进行权衡的旋钮。
五、总结
本文提出了改进扩散模型的结构框架,在无条件生成图像中可以获得比最先进的 GAN 更好的样本质量。最核心的是这篇论文提出了一个分类器梯度的思想去指导模型生成更符合我们需求的图像。而且还可以调整分类器梯度的规模,在多样性和保真度之间进行权衡。这些引导扩散模型可以减少 GAN 和扩散模型之间的采样时间差距,尽管扩散模型在采样期间仍然需要多次前向传递。最后,通过将引导与上采样相结合,我们可以进一步提高高分辨率条件图像合成的样本质量。
虽然扩散模型已经击败GAN在图像生成质量上,但仍然存在以下缺点:
尽管有DDIM和IDDPM各种加速采样的技术出现,但是仍然不如GAN采样的速度快;
Classifier guidance只针对有标签的数据,没有提供有效的策略来权衡未标记数据集的多样性和保真度。