扩散模型——3.Improved DDPM

 2023/07/25 

一、前言

本文提出了DDPM的几点缺陷：

1.DDPM在CIFAR-10和LSUN数据集上表现出比较好的结果，但是并不清楚在具有更高多样性的数据集（如imageNet）表现效果，实际上是不如BigGAN。

2.尚未证明 DDPM 可以实现与其他基于似然的模型竞争的对数似然性。对数似然性是生成建模中广泛使用的度量指标，一般认为优化对数似然会迫使生成模型捕获数据分布的所有模式。并且对数似然性的微小改进可以对样本质量和学习的特征表示产生显著的影响。所以不证明DDPM的对数似然性的后果就是，不知道DDPM是否能够捕获分布的所有模式。

基于这些特性，本文提出了如下几点改进工作：

1.该论文证明，即使在 ImageNet 等高多样性数据集上，DDPM 也可以实现与其他基于似然的模型相媲美的对数似然;

2.为了更紧密地优化变分下界（VLB），我们使用简单的重新参数化和混合学习目标来学习逆向过程方差(可学习的方差)，该混合学习目标将 VLB 与DDPM的简化目标相结合。并且使用混合学习目标，对比那些直接优化对数似然的模型来说，会使得模型得到了更好的对数似然。

3.作者发现直接优化对数似然，其实在训练期间会存在很多的梯度噪声。而作者使用了一种简单的重要性采样技术减少这种噪声并实现比混合目标更好的对数似然。

4.将学习到的方差纳入到模型之后，就可以用更少的步骤从模型中进行采样，而样本质量的变化很小，比起DDPM需要数百次前向传递才能产生良好的样本，但我们只需 50 次前向传递即可获得良好的样本，从而加快实际应用中的采样速度。后续也和DDIM进行了比较。

二、提高对数似然性（Log-likelihood）

在本节中探讨了对DDPM描述的算法的一些修改，这些修改结合起来，允许 DDPM 在图像数据集上实现更好的对数似然，这表明这些模型享有与其他基于似然的生成模型相同的好处。

1、可学习方差$\Sigma_\theta(x_t,t)$

在DDPM中方差是固定为$\textcolor{blue}{Σ_θ(x_t, t) = σ^2_t I}$,然而他们发现其实不学习的$\textcolor{blue}{\sigma_t}$无论是取$\textcolor{blue}{\beta_t}$，还是取$\textcolor{blue}{\tilde{\beta}_t}$产生的样本质量都大致相同。但其实，它们是$\textcolor{blue}{q(x_0)}$ 给出的方差的上限和下限。由下图，我们可以看出：这表明$\textcolor{blue}{\beta_t}$和$\textcolor{blue}{\tilde{\beta}_t}$几乎相等，除了 t = 0 附近，即模型处理难以察觉的细节的地方。此外，当我们逐渐增加扩散步骤，$\textcolor{blue}{\beta_t}$和$\textcolor{blue}{\tilde{\beta}_t}$在T比较大的扩散过程中似乎保持彼此接近。这表明，在无限扩散步骤的限制下，$\textcolor{blue}{\sigma_t}$的选择对于样本质量可能根本不重要。换句话说，当更扩散步骤增多时，模型平均值$\textcolor{blue}{μ_θ(x_t, t)}$ 比 $\textcolor{blue}{Σ_θ(x_t, t)}$ 更能决定分布。

虽然上述论点表明，为了样本质量，固定$\sigma_t$是一个合理的选择，但它没有提到对数似然。事实上，下图显示扩散过程的前几个步骤对变分下界的贡献最大（loss变化比较大）。因此，我们似乎可以通过使用更好的$Σ_θ(x_t, t)$选择来提高对数似然。为了实现这一点，我们必须学习$Σ_θ(x_t, t)$。

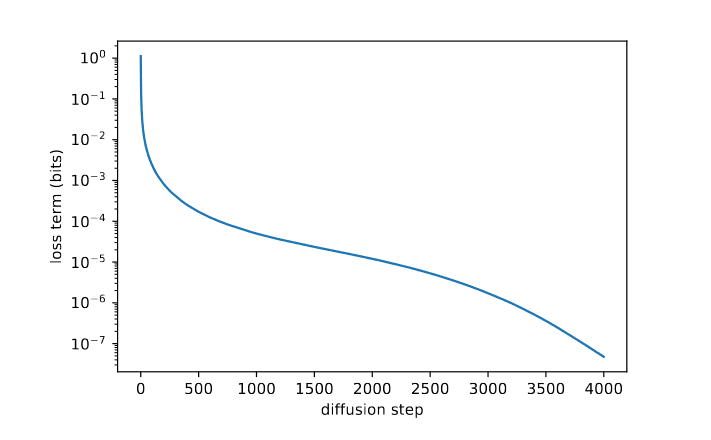
由图1,我们可以看出显示$Σ_θ(x_t, t)$的合理范围非常小，因此神经网络很难直接预测$Σ_θ(x_t, t)$，作者采用了将方差参数化为对数域中$\beta_t$和$\tilde{\beta}_t$之间的插值。就是让模型预测出一个向量 v，每个维度包含一个分量，我们将此输出转换为方差，如下所示：

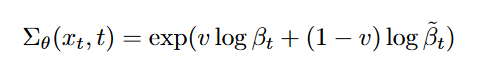
1692001848629

由于原本的$\mathcal{L}_{simple}$不依赖于$Σ_θ(x_t, t)$，因此作者定义了一个新的混合目标，$\lambda$取0.001：

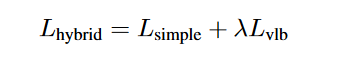
1692002047802

2、余弦加噪策略

作者发现DDPM所使用的线性噪声表。对于高分辨率图像效果很好，但对于分辨率 64 × 64 和 32 × 32 的图像来说效果不佳。前向噪声过程的末尾噪声太大，因此对样本质量没有太大贡献。这可以在图 3 中直观地看到。意思就是说使用线性噪声表，使得图像在前向过程后半段加噪的速度过快，导致在已经是随机噪声当中继续加噪，这使得后半段的加噪意义不大。而下图表现出余弦加噪的速度比较缓慢。

1692002600644

图 4 对比了这两种现象的结果，我们可以看到，当我们跳过多达 20% 的反向扩散过程时，使用线性噪声表训练的模型并没有变得更糟（通过 FID 测量），对于具有马尔可夫性质的反向去噪过程来说，去掉百分之20的扩散步骤都没有让FID数值增高（越低越好），说明线性加噪的后半段过程确实是没什么意义的，没意义还要按这个步长进行采样，也是白白增加采样时间，而且采样出来的效果也大差不差。

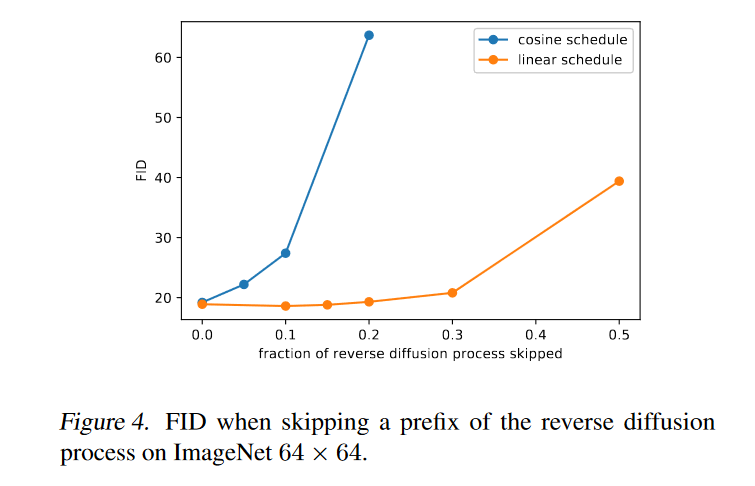
为了解决这个问题，作者根据$\bar{\alpha}_t$构建了一个不同的噪声表，名为余弦噪声表：

注：在实践中，我们将$β_t$限制为不大于 0.999，以防止在扩散过程结束时接近 t = T 时出现奇点。

余弦时间表设计为在过程中间有一个$\bar{\alpha}_t$的线性下降，同时在 t = 0 和 t = T 的极值附近变化很小，以防止噪声水平突然变化。图 5 显示了两个不同方案的噪声时间表的$\bar{\alpha}_t$进展情况。我们可以看到DDPM的线性时间表下降到零的速度要快得多，信息破坏的速度比余弦的要快。

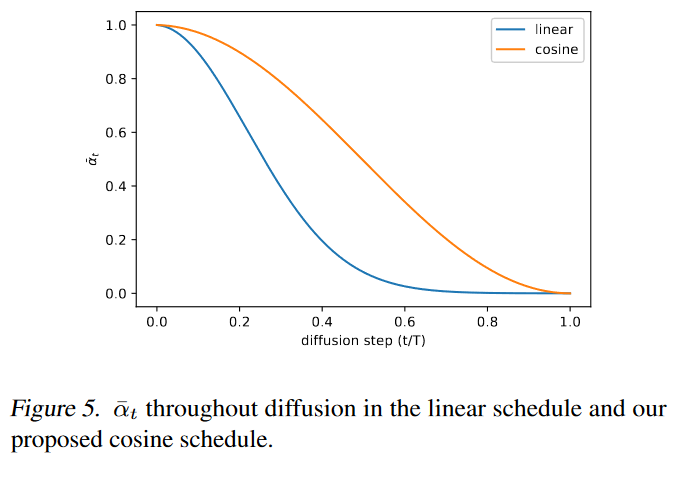
我们使用较小的偏移量 s 来防止 $β_t$ 在 t = 0 附近太小，因为作者发现在过程开始时存在少量噪声会使网络难以足够准确地进行预测。s设置为0.008。

3、减少梯度噪声

由于作者发现$L_{vlb}$在实践中其实是很难优化，至少在多样化的 ImageNet 64 × 64 数据集上是这样。图 6 显示了$L_{vlb}$和 $L_{hybrid}$的学习曲线。两条曲线都有噪声，但在给定相同训练时间的情况下，混合目标（$L_{hybrid}$）显然在训练集上实现了更好的对数似然。

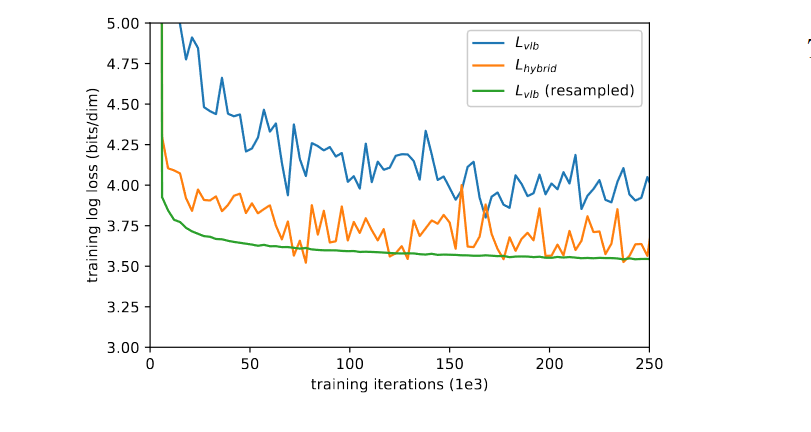
图7通过评估了分别使用$L_{vlb}$和 $L_{hybrid}$两个目标训练模型的梯度噪声尺度。从图7当中我们可以看出$L_{vlb}$的梯度比 $L_{hybrid}$的梯度噪声大得多。因此，在实际优化过程中，应当找到真正需要继续优化的点进行优化，因此提出了基于Loss的重要性才采样。

注意到$L_{vlb}$的不同项具有很大不同的大小（图 2），假设均匀采样 t 会在$L_{vlb}$目标中产生不必要的噪声。为了解决这个问题，作者采用重要性采样：

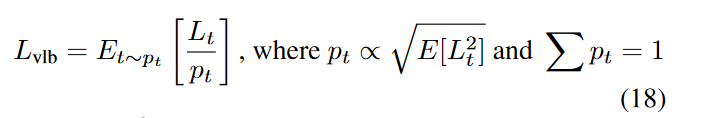
由于$E[L_t^2]$一开始是并不知道的，并且在整个训练过程中可能会发生变化，因此我们维护每个损失项的前 10 个值的历史记录，并在训练期间动态更新。在训练开始时，我们对 t 进行均匀采样，直到为每个 t ∈ [0, T − 1] 抽取 10 个样本。

有了这个重要性采样目标，就能够通过优化$L_{vlb}$来实现最佳对数似然。这可以在图 6 中看到，即 $L_{vlb}$(resampled)曲线。该图还显示，重要性采样目标的噪声比原始的均匀采样目标要少得多。而且作者发现，在直接优化噪声较小的$L_{hybrid}$目标时，重要性采样技术没有帮助。

补充：这里结合代码去看比较容易理解，在IDDPM官方代码的Image_train.py当中，我们可以看到作者定义了采样器：

进入create_named_schedule_sampler函数里面（resample.py），我们可以看到其中有均匀采样（uniform），或者是基于loss重要性采样方式（二阶动量平滑loss，loss-second-moment）：

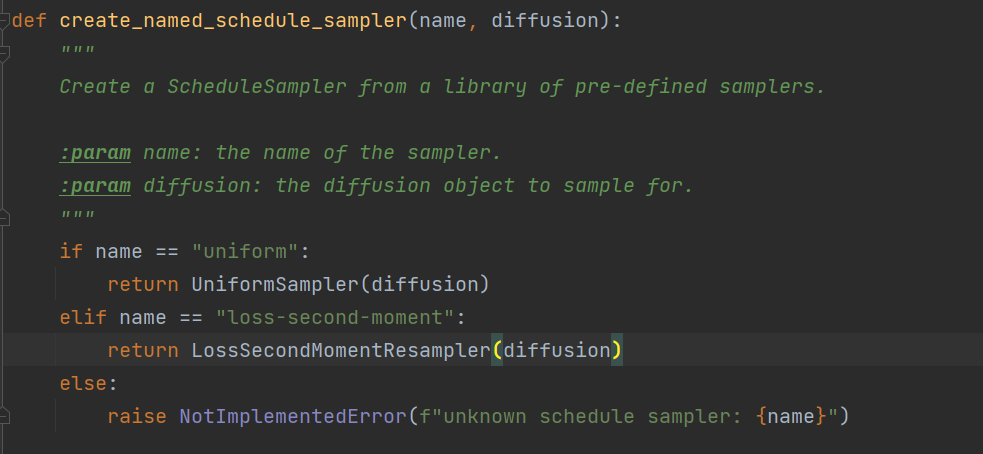
我们再进入LossSecondMomentResampler函数当中，我们就能看到作者是如何实现基于重要性采样的:

具体来说就是：

1.动态更新历史损失：该动态更新的历史损失，就是构造一个尺寸为[T, 10]的矩阵，即为整个扩散过程的T步存储10个最新的损失值（update_with_all_losses方法）；在将该历史损失矩阵所有的值填满前，先是用均匀采样对每个时间步都更新一遍，一直到所有时间步都存储了最新的10个历史损失为止。才计算其权重，不然前面的权重都是全一数组。

2.计算每个时间步的权重：在所有时间步上的历史损失都更新完毕以后（在填满之后），即(self._loss_counts == self.history_per_term).all()为True。基于每个时间步的10个历史损失计算随机采样的权重，为下一个step训练时更新时间步的采样权重；并且如果使用该类型的时间步sampler，在一个step中损失计算后，还需要调用update_with_local_losses函数将新计算得到的损失填入到历史损失矩阵最后端，并将最前端的最旧的历史损失弹出。

class LossSecondMomentResampler(LossAwareSampler):
    def __init__(self, diffusion, history_per_term=10, uniform_prob=0.001):
        self.diffusion = diffusion
        self.history_per_term = history_per_term
        self.uniform_prob = uniform_prob
        # 创建一个形状为[diffusion.num_timesteps, history_per_term]的全零数组_loss_history，用于存储损失的历史记录。
        self._loss_history = np.zeros(
            [diffusion.num_timesteps, history_per_term], dtype=np.float64
        )
        # 创建一个长度为diffusion.num_timesteps的全零数组_loss_counts，用于记录每个时间步的损失数量。
        self._loss_counts = np.zeros([diffusion.num_timesteps], dtype=np.int)
    # 用于计算每个时间步的权重
    def weights(self):
        # 如果还没有达到预定的历史记录数量，返回一个全一数组作为权重
        if not self._warmed_up():
            return np.ones([self.diffusion.num_timesteps], dtype=np.float64)
        # 计算损失历史记录的平方的均值的平方根，得到每个时间步的权重
        weights = np.sqrt(np.mean(self._loss_history ** 2, axis=-1))
        # 将权重归一化，使其总和为1
        weights /= np.sum(weights)
        # 将均匀概率乘以权重的总数减去1，并加上每个权重的均匀概率除以权重的数量
        weights *= 1 - self.uniform_prob
        weights += self.uniform_prob / len(weights)
        # 返回计算得到的权重
        return weights
    # 用于更新损失历史记录
    def update_with_all_losses(self, ts, losses):
        # 遍历传入的时间步和损失列表
        for t, loss in zip(ts, losses):
            # 如果某个时间步的损失数量达到了预定的历史记录数量
            if self._loss_counts[t] == self.history_per_term:
                # 将最旧的损失现移出历史记录，然后将新的损失项添加到历史记录的末尾
                self._loss_history[t, :-1] = self._loss_history[t, 1:]
                self._loss_history[t, -1] = loss
            # 如果某个时间步的损失数量还没有达到预定的历史记录数量
            else:
                # 将新的损失项添加到历史记录中，并将损失数量加1
                self._loss_history[t, self._loss_counts[t]] = loss
                self._loss_counts[t] += 1
    # 用于判断是否已经达到预定的历史记录数量。
    def _warmed_up(self):
        # 检查每个时间步的损失数量是否都等于预定的历史记录数量。
        # 如果所有时间步的损失数量都等于预定的历史记录数量，则返回True，表示已经达到预定的历史记录数量。
        # 否则，返回False，表示还没有达到预定的历史记录数量
        return (self._loss_counts == self.history_per_term).all()

最后，我们再根据sample得到每个批次随机选择的时间步以及权重：

然后再拿得到时间步去计算损失，最后利用权重加权求和。

关于重要性采样也可以看一下这篇文章：Importance Sampling (重要性采样)介绍 | 文艺数学君

4、实验结果以及消融实验

注：下面实验中$L_{simple}$表示的是DDPM的目标函数（均匀采样），而$L_{hybrid}$表示的是混合目标函数，$L_{vlb}$是改进后的基于loss的重要性采样目标函数。 $L_{vlb}$和 $L_{hybrid}$使用参数化学习到的方差$Σ_θ(x_t, t)$进行训练。

表 1 总结了在 ImageNet 64 × 64 上的消融结果。

表 2 展示了 CIFAR-10 的结果，在CIFAR-10中，原本的DDPM的效果已经很好了（针对FID而言），而在对数似然性（NLL）上来看效果不是最好的。

根据消融实验，使用 $L_{hybrid}$和余弦时间表提高了对数似然，同时保持类似的 FID 作为DDPM基线。优化$L_{vlb}$进一步提高对数似然，但代价是更高的 FID。所以作者通常更喜欢使用 $L_{hybrid}$而不是$L_{vlb}$，因为它可以在不牺牲样本质量的情况下提高可能性。

在表 3 中，将IDDPM的最佳的似然模型与之前的工作进行了比较，表明该模型在对数似然方面与最佳传统方法具有竞争力。

三、提高采样速度

对于使用 T 个扩散步骤训练的模型，我们通常会使用与训练期间使用的相同的 t 值序列 (1, 2, ..., T ) 进行采样（DDPM）。然而，也可以使用 t 值的任意子序列 S 进行采样(DDIM)。给定训练噪声表$\bar{\alpha}_{t}$ ，对于给定的序列 S，我们可以获得采样噪声表$\bar{\alpha}_{S_t}$，然后可以使用它来获得相应的采样方差。

现在，由于 $Σ_θ(x_{S_t} , S_t)$ 被参数化为$β_{S_t}$和$\tilde{β}_{S_t}$ 之间的范围，因此它将自动重新调整以适应较短的扩散过程。因此，我们可以将$p(x_{S_{t−1}} |x_{S_t} ) $计算为 $N (μ_θ(x_{S_t} , S_t), Σθ(x_{S_t} , S_t))$。

为了将采样步骤数从 T 减少到 K，我们使用 1 到 T（包括）之间的 K 个均匀间隔的实数，然后将每个结果数字舍入到最接近的整数。在图 8 中，我们评估了经过 4000 步数的扩散训练的$L_{hybrid}$模型和$L_{simple}$模型的FID，并且使用了25，50，100，500，1000的采样步数。

由此表可以发现，当使用较少的采样步骤时，具有固定 $\sigma$ 的 $L_{simple}$ 模型（具有较大的$σ^2_t = β_t$和较小的$σ^2_t=\tilde{\beta}_t$）在样本质量方面受到更多影响，而具有学习$\sigma$的$L_{hybrid}$模型则保持不变。高样品质量。使用此模型，100 个采样步骤足以为我们完全训练的模型实现接近最佳的 FID。还可以发现 DDIM 使用少于 50 个采样步骤生成更好的样本，但使用 50 个或更多步骤时生成更差的样本。有趣的是，DDIM 在训练开始时表现较差，但随着训练的继续，缩小了与其他采样器的差距。作者发现他们的跨步技术极大地降低了 DDIM 的性能，因此DDIM结果使用DDIM的恒定跨步。其中最终时间步长是$T − T /K + 1$而不是 T 。其他采样器在我们的跨步中表现稍好一些。

四、与GAN比较

作者为了使模型具有类条件，通过与时间步 t 相同的路径注入类信息。特别是，将类嵌入 $v_i$ 添加到时间步嵌入 $e_t$ 中，并将此嵌入传递到整个模型的残差块。

图 9 显示了来自较大模型的样本（具有 2.7 亿个参数、25 万次迭代的更大模型）。

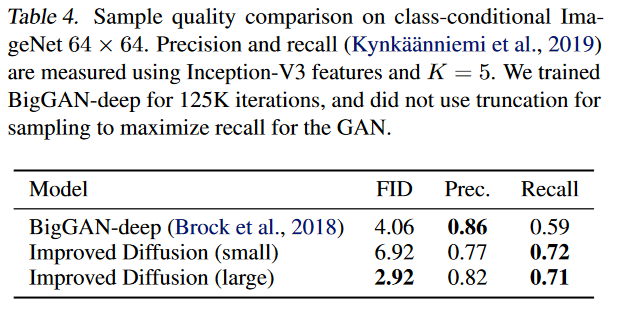
表 4 展示了IDDPM（small和large）与BigGAN的对比结果。我们发现 BigGAN-deep 在 FID 方面优于我们的较小模型，但在召回方面却表现不佳。这表明扩散模型比同类 GAN 更能覆盖分布模式。

五、缩放模型尺寸

在前面的部分中，展示了在不改变训练计算量的情况下改进对数似然和 FID 的算法更改。然而，现代机器学习的一个趋势是讲究个大力出奇迹（更大的模型和更多的训练时间往往会提高模型性能）。鉴于这一观察结果，作者还研究了 FID 和 NLL 如何根据训练计算进行扩展。我们的结果虽然是初步的，但表明随着训练计算的增加，DDPM 以可预测的方式改进。

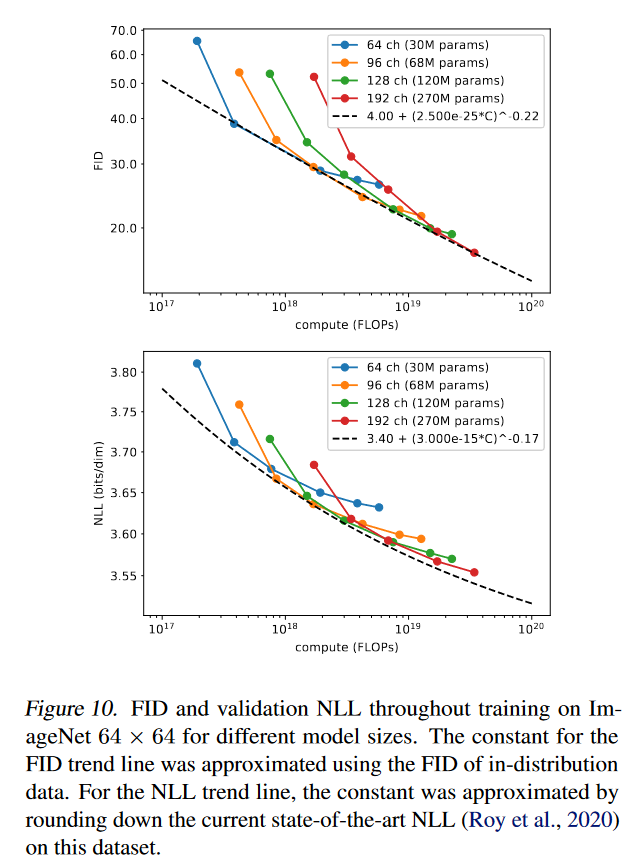
为了衡量性能如何随着训练计算而扩展，作者使用了$L_{hybrid}$目标在 ImageNet 64 × 64 上训练四个不同的模型。为了改变模型容量，在所有层上应用深度乘数，使得第一层具有 64、96、128 或 192 个通道。请注意，我们之前的实验在第一层使用了 128 个通道。由于每层的深度都会影响初始权重的规模，因此作者将每个模型的 Adam学习率缩放为 $1/\sqrt{通道乘数}$，使得 128 通道模型的学习率为 0.0001 (正如其他实验一样）。

图 10 显示了 FID 和 NLL 相对于理论训练计算的改进情况。FID 曲线在双对数图上看起来近似线性，表明 FID 根据幂律进行缩放（绘制为黑色虚线）。 NLL 曲线并不完全符合幂律，这表明验证 NLL 的扩展方式不如 FID。这可能是由多种因素引起的，例如 1) 此类扩散模型的不可约损失出乎意料地高，或 2) 模型对训练分布过度拟合。我们还注意到，这些模型通常无法实现最佳对数似然，因为它们是使用我们的$L_{hybrid}$目标进行训练的，而不是直接使用$L_{vlb}$ 进行训练，以保持良好的对数似然和样本质量。

六、总结

本篇文章证明了通过一些修改，DDPM 可以更快地采样并实现更好的对数似然，而对样本质量的影响很小。通过使用参数化和混合目标目标学习 $Σ_θ$ 可以提高对数似然性。这使得这些模型的对数似然性更接近其他基于对数似然性的模型。并且这种变化还可以以更少的步骤从这些模型中进行采样。并且DDPM 可以与 GAN 的样本质量相匹配，同时根据召回率衡量，可以实现更好的模式覆盖率。此外，作者还研究了 DDPM 如何随着可用训练计算量的变化而扩展，并发现更多的训练计算会带来更好的样本质量和对数似然。这些结果的结合使 DDPM 成为生成建模的一个有吸引力的选择，因为它们将良好的对数似然、高质量样本和相当快的采样与基础良好的固定训练目标结合起来，该目标可以通过训练计算轻松扩展。这些结果表明DDPMs是未来研究的一个有希望的方向（的确，后面的扩散模型很多都是基于IDDPM）。

七、其他

1、在ImageNet 256x256中采样

在类条件 ImageNet 256 × 256 上训练了两个模型。第一个是通常的扩散模型，直接对 256 × 256 图像进行建模。第二个模型通过将预训练的 64 × 64 模型 $p(x_{64}|y)$ 与另一个上采样扩散模型 $p(x_{256}|x_{64}, y)$ 链接起来将图像上采样到 256 × 256 来减少计算量。对于上采样模型，下采样图像 $x_{64}$为作为额外调节输入传递给 UNet。这类似于 VQ-VAE-2 ，它使用不同潜在分辨率的两个先验阶段来更有效地学习全局和局部特征。线性计划对于 256 × 256 图像效果更好，因此我们将其用于这些结果。表 5 总结了我们的结果。扩散模型仍然获得基于似然模型的最佳 FID，并大大缩小了与 GAN 的差距。